【中国发明,中国发明授权】一种抑制柔性机械臂振动的边界控制方法
无权-未缴年费 中国
- 申请号:
- CN201410675083.4
- 专利权人:
- 电子科技大学
- 授权公告日/公开日:
- 2016.01.13
- 专利有效期:
- 2014.11.21-2034.11.21
- 技术分类:
- B25:手动工具;轻便机动工具;手动器械的手柄;车间设备;机械手
- 转化方式:
- 转让
- 价值度指数:
-
- 54.0分
- 价格:
- 面议
- 专利信息&法律状态
- 专利自评
- 专利技术文档
- 价值度指数
- 发明人阵容
 著录项
著录项
- 申请号
- CN201410675083.4
- 申请日
- 20141121
- 公开/公告号
- CN104589344A
- 公开/公告日
- 20150506
- 申请/专利权人
- [电子科技大学]
- 发明/设计人
- [贺威, 杨川, 何修宇]
- 主分类号
- B25J9/16
- IPC分类号
- C12N 9/0008(2013.01) C12N 9/16
- CPC分类号
- C12N 9/0008(2013.01) C12N 9/16(2013.01)
- 分案申请地址
- 国省代码
- 四川(51)
- 颁证日
- G06T1/00
- 代理人
- [温利平]
 摘要
摘要
本发明公开了一种抑制柔性机械臂振动的边界控制方法,通过对柔性机械臂系统进行分析并建立数学模型,再结合数学模型设计出柔性机械臂系统的边界控制器,然后对带有控制作用的柔性机械臂系统进行稳定性分析,并仿真系统运动状态,根据仿真结果对系统的控制参数进行调整,使之最终达到设计要求。这样首先能够有效地抑制柔性机械臂在工作过程中的振动,其次,本发明在设计边界控制器时,增加了驱动柔性机械臂到达指定位置的功能,这样还能够实现柔性机械手臂的位置跟踪。
 法律状态
法律状态
| 法律状态公告日 | 20201030 |
| 法律状态 | 专利权的终止 |
| 法律状态信息 | 未缴年费专利权终止 IPC(主分类):B25J 9/16 专利号:ZL2014106750834 申请日:20141121 授权公告日:20160113 终止日期:20191121 |
| 法律状态公告日 | 20160113 |
| 法律状态 | 授权 |
| 法律状态信息 | 授权 |
| 法律状态公告日 | 20150527 |
| 法律状态 | 实质审查的生效 |
| 法律状态信息 | 实质审查的生效 IPC(主分类):B25J 9/16 申请日:20141121 |
| 法律状态公告日 | 20150506 |
| 法律状态 | 公开 |
| 法律状态信息 | 公开 |
 权利要求
权利要求
权利要求数量(1)
独立权利要求数量(1)
1.一种抑制柔性机械臂振动的边界控制方法,其特征在于,包 括以下步骤:
(1)、对柔性机械臂系统进行分析并建模
柔性机械臂系统的动能:
其中,I代表柔性机械臂系统的惯量,θ(t)代表柔性机械臂的偏 转角度,ρ代表柔性机械臂的密度,L是柔性机械臂的长度,y(x,t)代 表在位置x、时间t时柔性机械臂系统的位置,x∈[0,L]表示柔性机械 臂各个位置,t∈[0,∞]表示时间;
柔性机械臂系统的势能:
其中,E I表示柔性机械臂的弯曲刚度,T为柔性机械臂的张力, 表示在位置x、时间t时柔性机械臂系统的振动幅值;
边界控制对柔性机械臂系统的虚功:
其中,δ是变分符号,τ(t)为边界控制器;
再根据哈密顿原理(Hamilton principle),得到柔性机械臂系统的 数学模型;
其中,
在柔性机 械臂系统的数学模型中,公式(4)为柔性机械臂系统的控制方程, 公式(5)为柔性机械臂系统的边界条件;
(2)、设计边界控制器τ(t)
其中,θ d表示控制柔性机械臂到达的预设位置;k 1和k 2为控制 参数,可以通过预先训练得到,即:预先通过MATLAB软件仿真一 个柔性机械臂系统,结合控制方程(4)和边界条件(5)进行仿真训 练,其训练目标是保证柔性机械臂上各处的振动幅值小于加入控制前 振动幅值 的M%,;
(3)、在时刻t,采用位移传感器测量得到柔性机械臂的振动幅 值 采用倾角计测量得到偏转角θ(t);
(4)、将步骤(3)得到的实时参数 θ(t),控制参数k 1,k 2以 及θ d的值代入步骤(2),得到任意t时刻的边界控制器τ(t),驱动装置 再根据边界控制器τ(t)向柔性机械臂施加作用力,驱使柔性机械臂移 动到指定位置θ d,同时抑制系统振动。
1.一种抑制柔性机械臂振动的边界控制方法,其特征在于,包括以下步骤:
(1)、对柔性机械臂系统进行分析并建模
柔性机械臂系统的动能:
E k ( t ) = 1 2 I [ θ . ( t ) ] 2 + 1 2 ρ ∫ 0 L [ y . ( x , t ) ] 2 dx ; - - - ( 1 ) ]]>
θ . ( t ) = ∂ θ ( t ) / ∂ t ; ]]>
y . ( x , t ) = ∂ y ( x , t ) / ∂ t ; ]]>
其中,I代表柔性机械臂系统的惯量,θ(t)代表柔性机械臂的偏转角度,ρ代表柔性机械臂的密度,L是柔性机械臂的长度,y(x,t)代表在位置x、时间t时柔性机械臂系统的位置,x∈[0,L]表示柔性机械臂各个位置,t∈[0,∞]表示时间;
柔性机械臂系统的势能:
其中,EI表示柔性机械臂的弯曲刚度,T为柔性机械臂的张力,表示在位置x、时间t时柔性机械臂系统的振动幅值;
边界控制对柔性机械臂系统的虚功:
δW m = τ ( t ) δ y ′ ( 0 , t ) - - - ( 3 ) ]]>
其中,δ是变分符号,τ(t)为边界控制器;
再根据哈密顿原理(Hamilton principle),得到柔性机械臂系统的数学模型;
其中, y . . ( x , t ) = ∂ 2 y ( x , t ) / ∂ 2 t , y ′ ′ ( x , t ) = ∂ 2 y ( x , t ) / ∂ x 2 , ]]>
在柔性机械臂系统的数学模型中,公式(4)为柔性机械臂系统的控制方程,公式(5)为柔性机械臂系统的边界条件;
(2)、设计边界控制器τ(t)
τ ( t ) = - k 1 θ . ( t ) - k 2 [ θ ( t ) - θ d ] - - - ( 6 ) ]]>
其中,θd表示控制柔性机械臂到达的预设位置;k1和k2为控制参数,可以通过预先训练得到,即:预先通过MATLAB软件仿真一个柔性机械臂系统,结合控制方程(4)和边界条件(5)进行仿真训练,其训练目标是保证柔性机械臂上各处的振动幅值小于加入控制前振动幅值的M%,;
(3)、在时刻t,采用位移传感器测量得到柔性机械臂的振动幅值采用倾角计测量得到偏转角θ(t);
(4)、将步骤(3)得到的实时参数θ(t),控制参数k1,k2以及θd的值代入步骤(2),得到任意t时刻的边界控制器τ(t),驱动装置再根据边界控制器τ(t)向柔性机械臂施加作用力,驱使柔性机械臂移动到指定位置θd,同时抑制系统振动。
 说明书
说明书
技术领域
本发明属于自动控制技术领域,更为具体地讲,涉及一种抑制柔性机械臂振动的边界控制方法。
背景技术
机器人技术已经经历了半个多世纪的快速发展,其应用范围已从最初单纯的工业生产延伸到了以工业、医学、农业、建筑业以及军事等为背景的各个领域。然而,随着人类对机器人性能,如质量、效率、稳定性以及寿命等指标提出了更高的要求,作为其重要组成部分的机械手臂也面临着重大的挑战。传统机械手臂(刚性手臂)的设计和制造都是以尽可能大的刚度来实现对定位和其它操作的相关要求,因此不可避免地形成了质量笨重、灵活性差、功耗高以及功能简单等缺点。相比于传统质量重、体积大的刚性手臂,采用轻质材料的柔性机械臂更好地克服了以上缺点,其操作灵活、响应快速、性能稳定的特点,使之在各个领域都具有很高的应用价值。
然而,随着材料的轻型化,必然衍生出易于受外界环境干扰而导致性能下降的负面影响,自身的振动问题成为了研究柔性机械臂所面临的最大难点。同时,由外界扰动造成的不良振动,使得机械臂难以精确定位;大的形变也将会影响其机械性能,甚至损毁机械结构,造成重大损失。因此,振动的抑制是我们必须要考虑并解决的问题。在系统的动力学分析中,柔性机械臂是一个典型的分布式参数系统,其无穷维的特点将是后续设计过程中的难点。
目前国内很多基于分布式参数系统的控制策略得到了充分地研究和发展,其中包括:变结构控制法、滑模控制法、基于能量的鲁棒控制、分布式控制和边界控制等。作为典型的非线性系统,滑模控制在柔性机械手臂的控制方面得到了一定的应用,且能表现出良好的控制效果和鲁棒性。例如专利号为201210052088.2的发明专利就采用将观测器与滑模控制相结合的策略,以达到对机械手臂的有效控制;以及专利号为201210052283.5的发明专利对欠驱动双耦合电机运用滑模控制方法实现所需的跟踪控制。但滑模控制不可避免地会引 起抖阵现象,降低控制精度,激发建模时被忽略的高频部分,且目前对滑模控制中如何设计优良的滑模面以产生稳定的滑模动态尚未得出十分有效的方法。边界控制作为一种新兴的控制方法,其应用也越来越广,例如将边界控制法应用在传送带的振动控制中,用以处理边界扰动和分布式扰动对系统造成的不良影响。抑制振动是控制理论的基本要求之一,而此种应用也仅仅局限在对系统振动的控制上,而针对工业机械手臂这类既需要抑制振动又需要控制角度的系统,目前的研究则显得十分有限。相对于其他控制方法而言,边界控制不仅能有效避免滑模控制中因忽略高频模态而引发的溢出效应,且不需要类似于分布式控制中利用大量的传感器去采集模态,大大减少了成本,因而得到了不断深入的研究和发展。
发明内容
本发明的目的在于克服现有技术的不足,提供一种抑制柔性机械臂振动的边界控制方法,通过设计合理的边界控制器使柔性机械臂系统达到稳定有界状态,从而实现对机械臂精确、稳定的控制。
为实现上述发明目的,本发明一种抑制柔性机械臂振动的边界控制方法,其特征在于,包括以下步骤:
(1)、对柔性机械臂系统进行分析并建模
柔性机械臂系统的动能:
E k ( t ) = 1 2 I [ θ · ( t ) ] 2 + 1 2 ρ ∫ 0 L [ y · ( x , t ) ] 2 dx ; - - - ( 1 ) ]]>
θ · ( t ) = ∂ θ ( t ) / ∂ t ; ]]>
y · ( x , t ) = ∂ y ( x , t ) / ∂ t ; ]]>
其中,I代表柔性机械臂的惯量,θ(t)代表柔性机械臂的偏转角度,ρ代表柔性机械臂的密度,L是柔性机械臂的长度,y(x,t)代表在位置x、时间t时柔性机械臂的位置,x∈[0,L]表示柔性机械臂各个位置,t∈[0,∞)表示时间;
柔性机械臂系统的势能:
其中,EI表示柔性机械臂的弯曲刚度,T为柔性机械臂的张力,表示在位置x、时间t时柔性机械臂的振动幅值;
边界控制对柔性机械臂系统的虚功:
δWm=τ(t)δy′(0,t) (3)
其中,δ是变分符号,τ(t)为边界控制器;
再根据哈密顿原理(Hamilton principle),得到柔性机械臂系统的数学模型:
其中, y · · ( x , t ) = ∂ 2 y ( x , t ) / ∂ 2 t , y ′ ′ ( x , t ) = ∂ 2 y ( x , t ) / ∂ x 2 , ]]>在柔性机械臂系统的数学模型中,公式(4)为柔性机械臂系统的控制方程,公式(5)为柔性机械臂系统的边界条件;
(2)、设计边界控制器τ(t)
τ ( t ) = - k 1 θ · ( t ) - k 2 [ θ ( t ) - θ d ] - - - ( 6 ) ]]>
其中,θd表示控制柔性机械臂到达的预设位置;k1和k2为控制参数,可以通过预先训练得到,即:预先通过MATLAB软件仿真一个柔性机械臂系统,结合控制方程(4)和边界条件(5)进行仿真训练,其训练目标是保证柔性机械臂上各处的振动幅值量小于加入控制前振动幅值的M%,0≤M<100;
(3)、在时刻t,采用移位传感器测量得到柔性机械臂的振动幅值采用倾角计测量得到偏转角θ(t);
(4)、将步骤(3)得到的实时参数θ(t),控制参数k1,k2以及θd的值及代入步骤(2),得到任意t时刻的边界控制器τ(t),驱动装置再根据边界控制τ(t)向柔性机械臂施加作用力,驱使柔性机械臂移动到指定位置θd,同时抑制系统 振动。
本发明的发明目的是这样实现的:
本发明抑制柔性机械臂振动的边界控制方法,通过对柔性机械臂系统进行分析并建立数学模型,再结合数学模型设计出柔性机械臂系统的边界控制器,然后对带有控制作用的柔性机械臂系统进行稳定性分析,并仿真系统运动状态,根据仿真结果对系统的控制参数进行调整,使之最终达到设计要求。这样首先能够有效地抑制柔性机械臂在工作过程中的振动,其次,本发明在设计边界控制器时,增加了驱动柔性机械臂到达指定位置的功能,这样还能够实现柔性机械手臂的位置跟踪。
同时,本发明抑制柔性机械臂振动的边界控制方法还具有以下有益效果:
(1)、设计了一个基于边界控制算法的控制器,通过在柔性机械臂末端加入一个控制力,使该控制器不仅能抑制柔性机械臂的弹性振动,而且还能够实现柔性机械手臂的位置跟踪;其次,控制器功能的实现过程只需较少的传感器和执行器,具有很好的应用前景;
(2)、作为本发明的一步改进,将边界控制器设置在柔性机械臂末端,改变了置于顶端的传统方式,从而更容易检测柔性机械臂信号,以配合工程应用。
附图说明
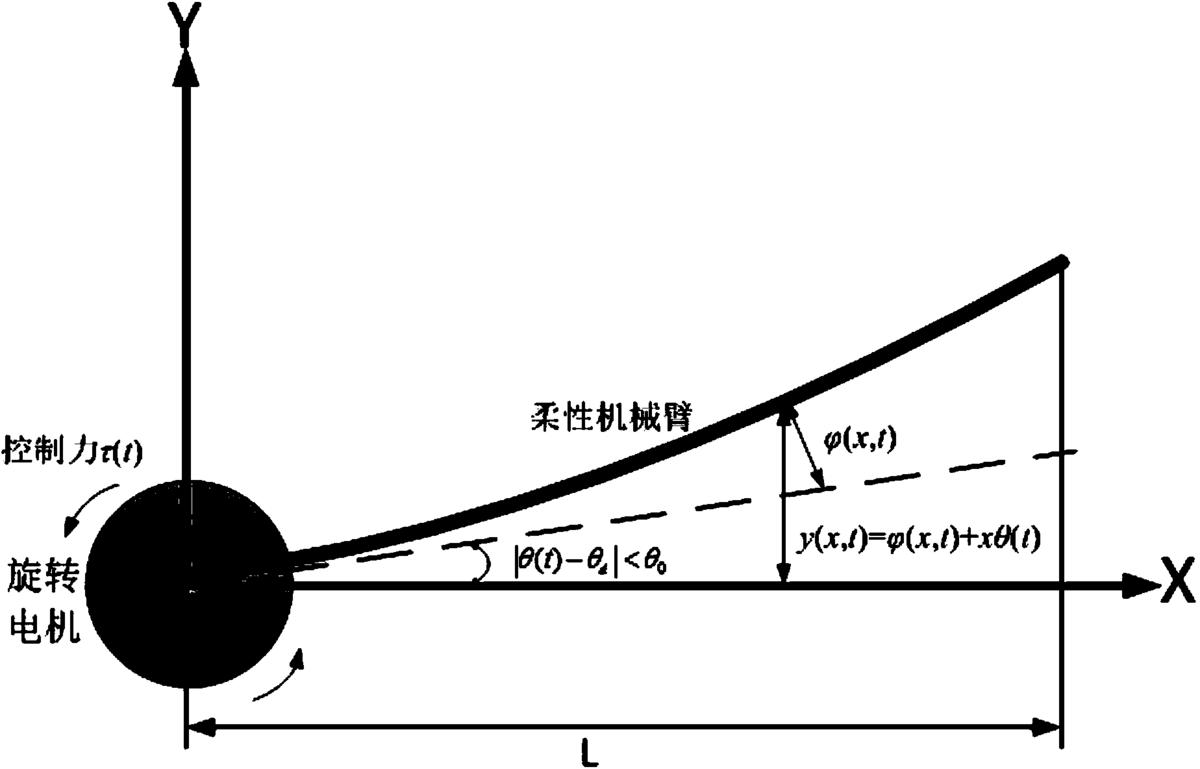
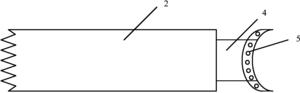
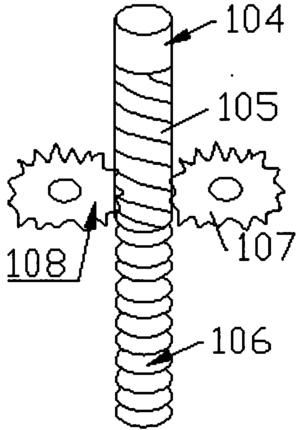
图1是柔性机械臂运行示意图;
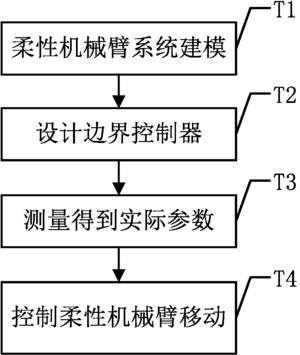
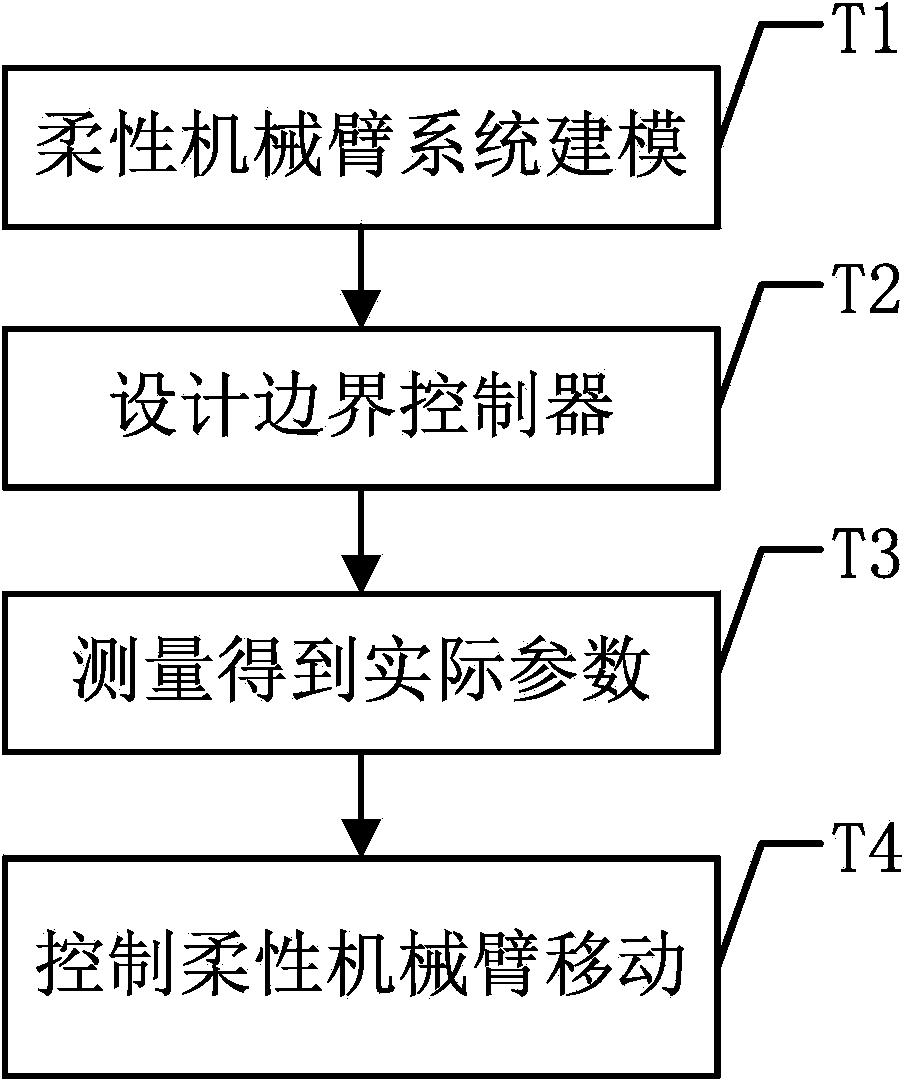
图2是本发明抑制柔性机械臂振动的边界控制方法的流程图;
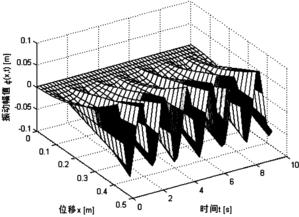
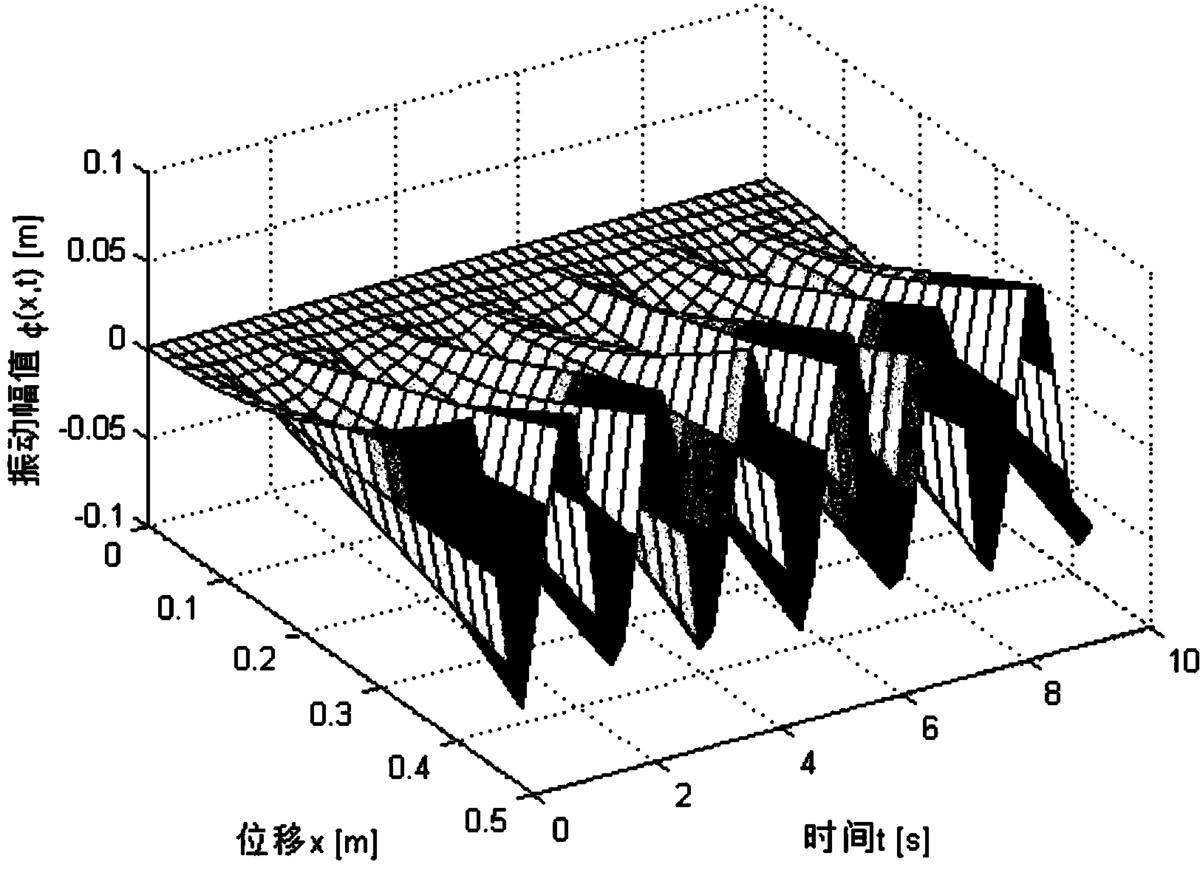
图3是本发明未加入边界控制时,柔性机械臂系统的振动仿真图;
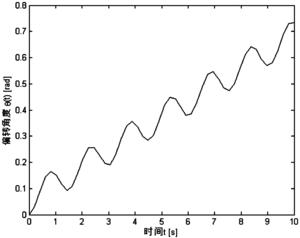
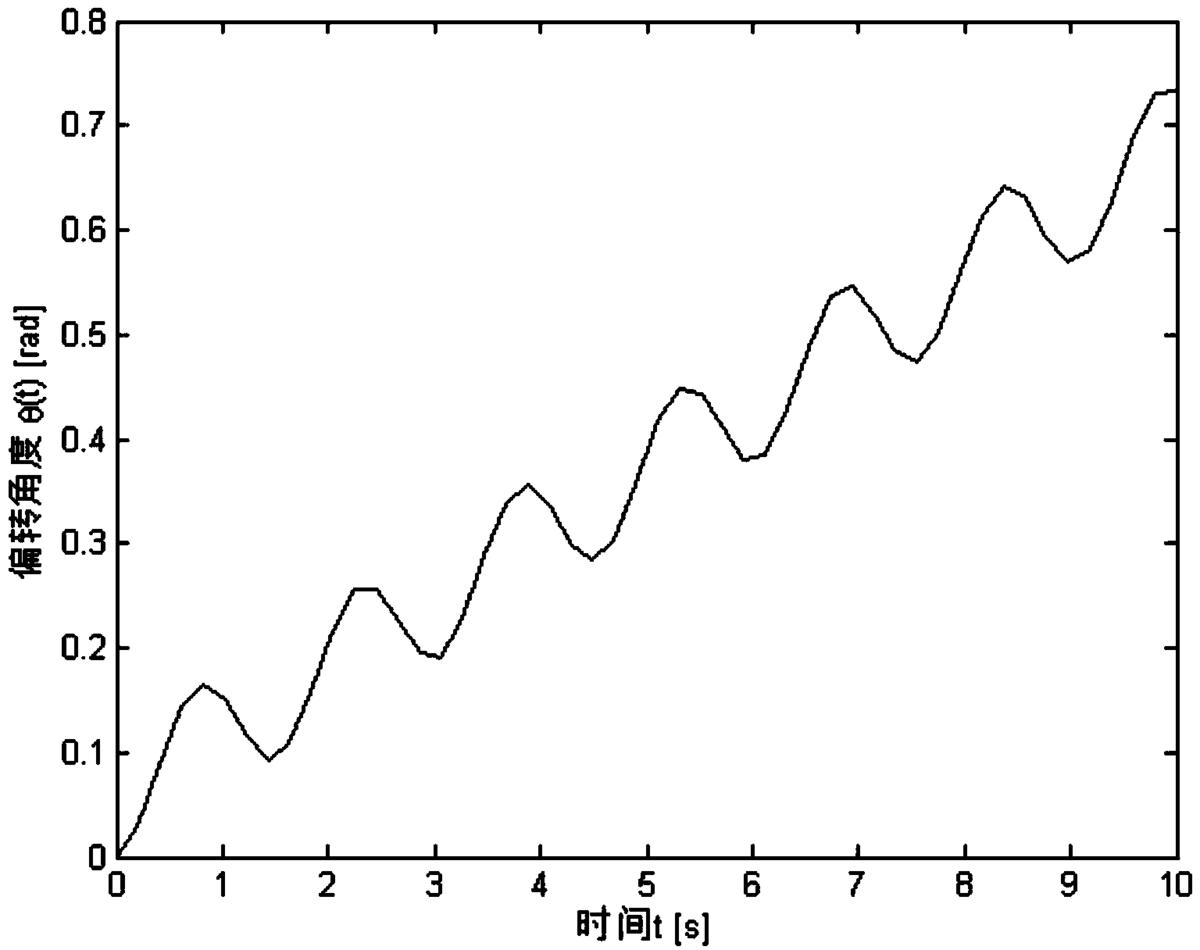
图4是本发明未加入边界控制时,柔性机械臂系统的角度仿真图;
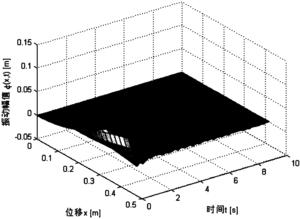
图5是本发明加入边界控制后,柔性机械臂系统的振动仿真图;
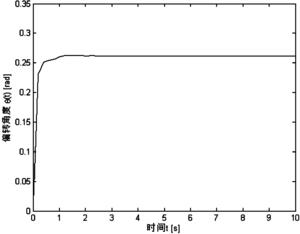
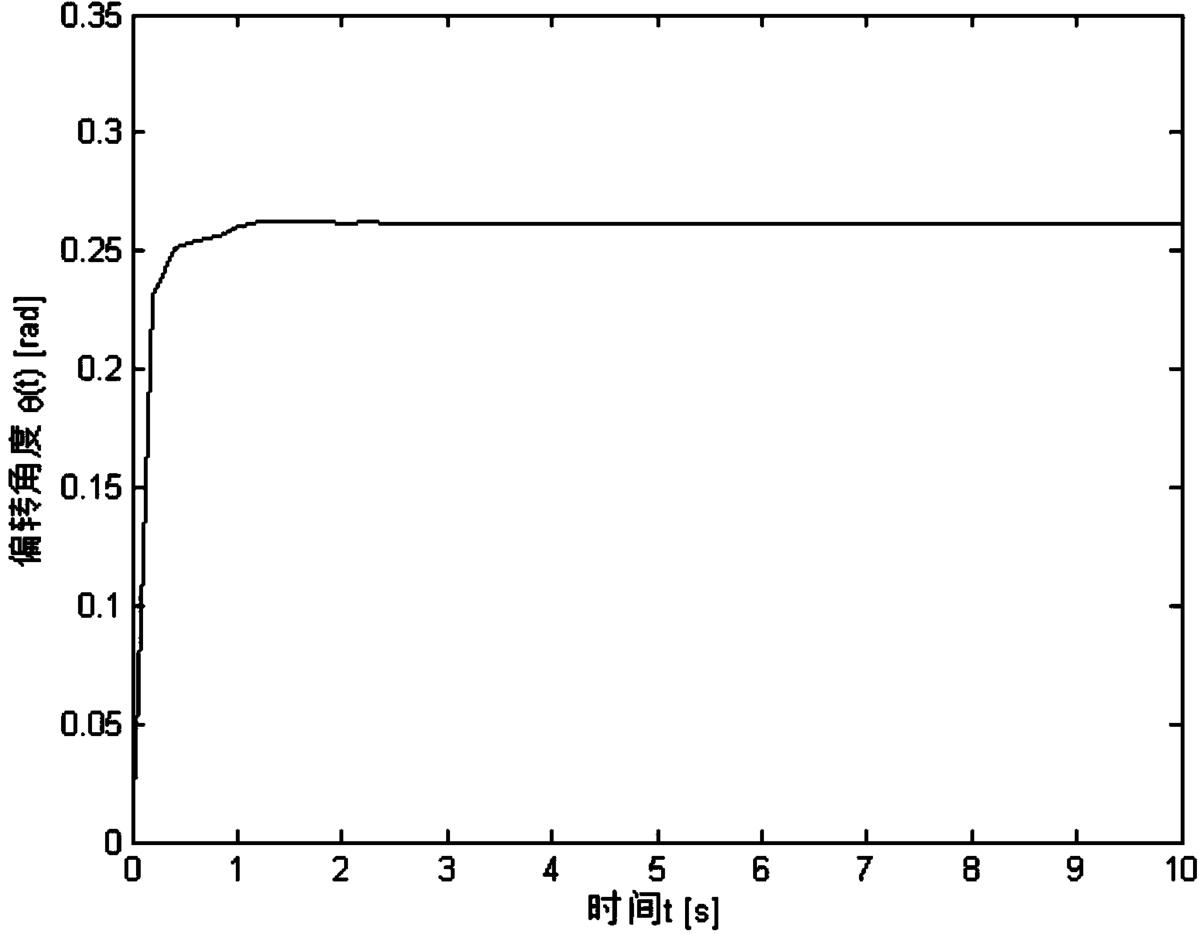
图6是本发明加入边界控制后,柔性机械臂系统的角度仿真图;
图7是边界控制器的控制输入仿真图。
具体实施方式
下面结合附图对本发明的具体实施方式进行描述,以便本领域的技术人员更好地理解本发明。需要特别提醒注意的是,在以下的描述中,当已知功能和设计的详细描述也许会淡化本发明的主要内容时,这些描述在这里将被忽略。
实施例
为了更有条理地说明本发明的技术内容,首先对柔性机械臂结构及控制系统工作原理进行介绍。如图1所示,柔性机械臂系统结构主要由机械手臂和旋转电机构成,边界控制器τ(t)在图1中用控制力τ(t)来简化表示,主要由传感器、控制器和驱动装置构成。传感器包含位移传感器和倾角测量计,用于对机械手臂的实时参数进行测量,本实施例中,位移传感器测量柔性机械臂的振动幅值 而倾角计测量柔性机械臂的偏转角θ(t),边界控制器τ(t)再根据上述参数,计算得到控制力,从而以驱动电机做出相应控制动作,实现角度控制以及振动抑制。
图2是本发明抑制柔性机械臂振动的边界控制方法的流程图。
在本实施例中,如图2所示,本发明一种抑制柔性机械臂振动的边界控制方法,包括以下步骤:
T1、对柔性机械臂系统进行分析并建模
柔性机械臂系统的动能:
E k ( t ) = 1 2 I [ θ · ( t ) ] 2 + 1 2 ρ ∫ 0 L [ y · ( x , t ) ] 2 dx ; - - - ( 1 ) ]]>
θ · ( t ) = ∂ θ ( t ) / ∂ t ; ]]>
y · ( x , t ) = ∂ y ( x , t ) / ∂ t ; ]]>
其中,I代表柔性机械臂的惯量,θ(t)代表柔性机械臂的偏转角度,ρ代表柔性机械臂的密度,L是柔性机械臂的长度,y(x,t)代表在位置x、时间t时柔性机械臂的位置,x∈[0,L]表示柔性机械臂各个位置,t∈[0,∞)表示时间;
柔性机械臂系统的势能:
其中,EI表示柔性机械臂的弯曲刚度,T为柔性机械臂的张力,表示在位置x、时间t时柔性机械臂的振动幅值;
边界控制对柔性机械臂系统的虚功:
δWm=τ(t)δy′(0,t) (3)
其中,δ是变分符号,τ(t)为边界控制器;
再根据哈密顿原理(Hamilton principle),得到柔性机械臂系统的数学模型:
其中, y · · ( x , t ) = ∂ 2 y ( x , t ) / ∂ 2 t , y ′ ′ ( x , t ) = ∂ 2 y ( x , t ) / ∂ x 2 , ]]>在柔性机械臂系统的数学模型中,公式(4)为柔性机械臂系统的控制方程,公式(5)为柔性机械臂系统的边界条件;
柔性机械臂系统的数学模型建立后,需要确定模型的相关参数,并结合参数控制柔性机械臂系统运行,在下面步骤中进行了详细说明:
T2、设计边界控制器τ(t)
设计边界控制器τ(t)时,需要考虑控制柔性机械臂到达指定位置θd的功能,即在保证柔性机械臂系统稳定的前提下,边界控制器对柔性机械臂系统的不良振动加以抑制以实现最小化振动的效果,并同时控制柔性机械臂到达指定位置θd。基于此,将边界控制器τ(t)设计为:
τ ( t ) = - k 1 θ · ( t ) - k 2 [ θ ( t ) - θ d ] - - - ( 6 ) ]]>
其中,k1和k2为控制参数,θd表示控制柔性机械臂到达的预设位置;
本实施例中,控制参数k1和k2可以通过预先训练得到,即:预先通过MATLAB软件仿真一个柔性机械臂系统,结合控制方程(4)和边界条件(5)进行仿真训练,其训练目标是保证柔性机械臂上各处的振动幅值小于加入控制前振动幅值的M%,0≤M<100,在本实施例中M=5。因此,得到满足训练目标的k1、k2即为本发明所需的控制参数;
T3、获取柔性机械臂移动时的实时参数
在时刻t,根据设定的初始条件,采用位移传感器测量得到柔性机械臂的振动幅值采用倾角计测量得到偏转角θ(t),对角度θ(t)求取一阶时间的导数得到
T4、控制柔性机械臂移动到指定位置
将步骤T3得到的实时参数θ(t),控制参数k1,k2和预设的θd值一起代入步骤T2得到任意时刻t的边界控制器τ(t),驱动装置再根据边界控制τ(t)向柔性机械臂施加作用力,驱使柔性机械臂移动到指定位置θd,同时抑制系统振动。
为说明本发明的实用性,下面对柔性机械臂系统进行稳定性验证
定义柔性机械臂系统的Lyapunov(李雅普诺夫)函数V(t):
V(t)=Eb(t)+k2[θ(t)-θd]2 (7)
其中,
对V(t)求时间的导数,得到:
V · ( t ) = E · b ( t ) + k 2 [ θ ( t ) - θ d ] θ · ( t ) - - - ( 8 ) ]]>
对Eb(t)求时间导数,得到:
将控制方程式(4)和边界条件式(5)代入到式(9)中,求解得到:
再将代入到式(8),得到:通过验证具有负定性,同时验证V(t)具有正定性,从而得到柔性机械臂系统能达到稳定且柔性机械臂系统状态最终收敛于0,进一步说明设计的控制器具有有效地控制作用;
验证为负定性的方法为:
由于则要使满足负定条件,前提必须有k1>0。此时再分两类情况讨论负定性,即:
Ta)、当时
根据等式得到再将代入到τ(t),可得:
τ(t)=-k2[θ(t)-θd] (10)
此时,边界控制器τ(t)为一个常数,将τ(t)代入控制方程式(4)和边界条件式(5)后,柔性机械臂系统模型可以改写为:
对于修改的柔性机械臂系统模型,通过分离变量法来进一步分析稳定性。为达到分离变量的目的,将既与位移x又与时间t相关的振动幅值拆分成仅包含一个自变量的Φ(x)和Q(t)之积,既定义:
将代入到控制方程式(11)中,得到:
Φ ′ ′ ′ ′ ( x , t ) Φ ( x , t ) · E I ρ - Φ ′ ′ ( x , t ) Φ ( x , t ) · T ρ = - θ · · ( t ) θ ( t ) - - - ( 13 ) ]]>
令 Φ ′ ′ ′ ′ ( x , t ) Φ ( x , t ) · E I ρ - Φ ′ ′ ( x , t ) Φ ( x , t ) · T ρ = - θ · · ( t ) θ ( t ) = K , ]]>则式(13)可以改写为:
θ · · ( t ) + Kθ ( t ) = 0 ]]>
Φ ′ ′ ′ ′ ( x ) - Φ ′ ′ ( x , t ) · T E I = KΦ ( x ) · ρ E I - - - ( 14 ) ]]>
将和τ(t)代入到边界条件式(12)中,得到:
Φ(0)=0,Φ′(0)=0
Φ ′ ′ ( L ) = 0 , Φ ′ ′ ′ ( L ) = T E I Φ ′ ( L ) - - - ( 15 ) ]]>
结合式(14)和(15),讨论不同K值所对应的情况,如下:
a)、当K=0时,令则通过求解式(14),可得:
Φ(x)=C1+C2x+C3e-βx+C4eβx (16)
其中,C1~C4是上述解中包含的待定系数。将式(16)代入到式(15)中,有:
C 1 + C 3 + C 4 = 0 C 2 - β C 3 + β C 4 = 0 e - βL C 3 + e βL C 4 = 0 β 3 C 2 = 0 - - - ( 17 ) ]]>
将等式(17)改写为: 1 0 1 1 0 1 β β 0 0 e βL e βL 0 β 3 0 0 C 1 C 2 C 3 C 4 = 0 - - - ( 18 ) ]]>
对等式(18)的系数矩阵求行列式,即: | D | = 1 0 1 1 0 1 β β 0 0 e βL e βL 0 β 3 0 0 , ]]>得到:|D|=-β3e-βL,行列式|D|<0,因此,当K=0时,等式(17)中的参数C1=C2=C3=C4=0,即解式(16)是无效解;
b)、当K<0时,令K=-ω2,则式(13)=K可以改写为:
EIΦ″″(x)-TΦ″(x)+ρω2Φ(x)=0 (19)
通过求解式(19)可得:
Φ(x)=C1e-ax+C2eax+C3e-bx+C4ebx (20)
其中, a = 2 2 β 2 + β 4 - 4 ρ ω 2 E I ]]>和 b = 2 2 β 2 - β 4 - 4 ρ ω 2 E I ; ]]>
将等式(20)代入到等式(15)中,可得:
C 1 + C 2 + C 3 + C 4 = 0 - aC 1 + a C 2 - b C 3 + b C 4 = 0 a 2 e - aL C 1 + a 2 e aL C 2 + b 2 e - bL C 3 + b 2 e bL C 4 = 0 a ( β 2 - a 2 ) e - aL C 1 - a ( β 2 - a 2 ) e aL C 2 + b ( β 2 - b 2 ) e - bL C 3 - b ( β 2 - b 2 ) e bL C 4 = 0 - - - ( 21 ) ]]>
同理可得到系数矩阵行列式|D|如下:
| D | = 4 a 2 b 2 ( ae - bL - be - aL ) [ b sinh ( aL ) - a sin ( bL ) ] + 4 ab [ b 2 cosh ( aL ) - a 2 cosh ( bL ) ] ( b 2 e - bL - a 2 e - aL ) + 4 a b 3 ( a - b ) [ a sinh ( aL ) cosh ( bL ) - b cosh ( aL ) sinh ( bL ) ] - - - ( 22 ) ]]>
根据式(22)可得到行列式|D|>0,因此,当K<0时,等式(21)中的参数C1=C2=C3=C4=0,即解式(20)也是无效解;
c)、当K>0时,令K=ω2,则式(13)=K可以改写为:
EIΦ″″(x)-TΦ″(x)-ρω2Φ(x)=0 (23)
通过求解式(23)可得:
Φ(x)=C1e-ax+C2eax+C3cos(bx)+C4sin(bx) (24)
其中, a = 2 2 β 2 + β 4 + 4 ρ ω 2 E I ]]>和 b = 2 2 β 4 + 4 ρ ω 2 E I - β 2 . ]]>
将等式(24)代入到等式(15),可得:
同理可得到系数矩阵行列式|D|如下:
| D | = a 5 b sinh ( aL ) cos ( bL ) + ab 2 sin ( bL ) [ a 2 b sin ( bL ) + ab 2 e - aL ] + ab 3 cosh ( aL ) [ b cos ( bL ) + a 2 e - aL ] - a 2 b 4 sin ( aL ) cosh ( aL ) + a 3 b cos ( bL ) [ b cos ( bL ) + a 2 e - aL ] + a 2 b sinh ( aL ) [ a 2 b sin ( bL ) + ab 2 e - aL ] - - - ( 26 ) ]]>
根据式(26)可得行列式|D|>0,因此,当K>0时,等式(25)中的参数C1=C2=C3=C4=0,即解式(24)也是无效解;
综上所述,当时,解Φ(x)中的参数C1=C2=C3=C4=0恒成立,即Φ(x)=0没有意义;
Tb)、当时,则柔性机械臂系统具有负定性;
验证Lyapunov函数V(t)的正定性:
根据定义的系统Lyapunov函数:V(t)=Eb(t)+k2[θ(t)-θd]2
首先,第一项是各个正数项之和,即:Eb(t)>0;
然后,第二项是平方项,满足:当k2>0时,有k2[θ(t)-θd]2≥0,
因此,V(t)=Eb(t)+k2[θ(t)-θd]2>0。所以,当k2>0时,V(t)满足正定性条件;
综合分类讨论的结果,Lyapunov函数V(t)是正定的,且是负定的,因此我们做出结论:柔性机械臂系统具有稳定性,且柔性机械臂系统状态将最终收敛于0。
为了说明本发明的有益效果,对本发明的实施进行了仿真验证。
本实施例中,通过Matlab仿真软件对柔性机械臂系统进行仿真时,在给出了初值条件的情况下,此时的仿真只取决于建模时的控制方程与边界条件,从而作出系统在自由运动条件下的振动幅值与角度位置图像。在不加控制作用时, 系统将会呈现出自动运动的状态,表现为在外界环境的影响下,柔性机械臂出现较大的振动偏移,且角度也将不受控制地增大。为了达到控制目的,我们将在系统中引入控制器τ(t),为了使加入控制器τ(t)后的系统能保持稳定,我们已经推导出控制参数满足k1>0,k2>0的条件。此时,我们将结合k1,k2的范围,对加入控制器后的系统进行仿真,得到在控制器的作用下,系统受控的振动与角度图像。
本实施例中,先对不加入边界控制的柔性机械臂系统进行仿真,柔性机械臂系统的振动仿真图和角度仿真图分别如图3和图4所示;
如图3所示,对于不加控制作用的柔性机械臂,在外界环境的影响下,系统出现了严重的震荡,能够形成0.07m的振动幅值。与此对应,从仿真图4中可以看出,偏转角度将随着系统的等幅震荡而出现波浪式增大,并最终远远偏离期望的角度θd(设定为30°≈0.52rad)。将两幅仿真图结合起来分析,可以得出:在不加控制时,系统位置(角度)将逐渐增大,且在增大的同时伴随着系统的持续震荡。此时,不良振动和形变将对系统性能造成严重破坏,导致系统不稳定、影响定位需求,甚至损毁机械结构。因此,在设计控制器时,必须考虑抑制甚至彻底消除振动的影响;
然后再对加入边界控制的柔性机械臂系统进行仿真,其对应的仿真图和角度仿真图分别如图5和图6所示;
如图5所示,在引入控制作用后,系统偏移量迅速下降,大约2s时接近于0,并最终能使系统在它的平衡位置保持稳定,机械臂振动得到了有效抑制。结合图6所示,在2s时系统位置(角度)达到设定值(设定为30°≈0.52rad),并保持恒定,这说明了设计的控制器有着良好的控制性能,系统的不稳定状态能得到显著抑制,能够满意地达到我们所需效果。从而,实现了快速驱动系统到达预 定位置的同时抑制振动的目的。
图7是边界控制器的控制输入仿真图。从稳定性分析过程中,我们得知柔性机械臂系统状态在边界控制器τ(t)的作用下最终有界,柔性机械臂系统能保持在稳定状态下运行,而根据Lyapunov法可知,此时的边界控制器τ(t)也将有界。如图7所示,直观地反映了边界控制器τ(t)的控制输入的有界性,从而进一步证明了整个控制器的有效性。
尽管上面对本发明说明性的具体实施方式进行了描述,以便于本技术领域的技术人员理解本发明,但应该清楚,本发明不限于具体实施方式的范围,对本技术领域的普通技术人员来讲,只要各种变化在所附的权利要求限定和确定的本发明的精神和范围内,这些变化是显而易见的,一切利用本发明构思的发明创造均在保护之列。
 价值度评估
价值度评估
技术价值
经济价值
法律价值
0 0 054.0分
0 50 75 100专利价值度是通过科学的评估模
型对专利价值进行量化的结果,
基于专利大数据针对专利总体特
征指标利用计算机自动化技术对
待评估专利进行高效、智能化的
分析,从技术、经济和法律价值
三个层面构建专利价值评估体
系,可以有效提升专利价值评估
的质量和效率。
总评:54.0分
该专利价值中等 (仅供参考)
本专利文献中包含【3 个技术分类】,从一定程度上而言上述指标的数值越大可以反映出所述专利的技术保护及应用范围越广。 【专利权的维持时间6 年】专利权的维持时间越长,其价值对于权利人而言越高。
技术价值 31.0
该指标主要从专利申请的著录信息、法律事件等内容中挖掘其技术价值,专利类型、独立权利要求数量、无效请求次数等内容均可反映出专利的技术性价值。 技术创新是专利申请的核心,若您需要进行技术借鉴或寻找可合作的项目,推荐您重点关注该指标。
部分指标包括:
授权周期(发明)
13 个月独立权利要求数量
0 个从属权利要求数量
0 个说明书页数
10 页实施例个数
0 个发明人数量
3 个被引用次数
0 次引用文献数量
0 个优先权个数
0 个技术分类数量
3 个无效请求次数
0 个分案子案个数
0 个同族专利数
0 个专利获奖情况
无保密专利的解密
否经济价值 7.0
该指标主要指示了专利技术在商品化、产业化及市场化过程中可能带来的预期利益。 专利技术只有转化成生产力才能体现其经济价值,专利技术的许可、转让、质押次数等指标均是其经济价值的表征。 因此,若您希望找到行业内的运用广泛的热点专利技术及侵权诉讼中的涉案专利,推荐您重点关注该指标。
部分指标包括:
申请人数量
1申请人类型
院校许可备案
0 次权利质押
0 次权利转移
0 个海关备案
否法律价值 16.0
该指标主要从专利权的稳定性角度评议其价值。专利权是一种垄断权,但其在法律保护的期间和范围内才有效。 专利权的存续时间、当前的法律状态可反映出其法律价值。故而,若您准备找寻权属稳定且专利权人非常重视的专利技术,推荐您关注该指标。
部分指标包括:
存活期/维持时间
6法律状态
无权-未缴年费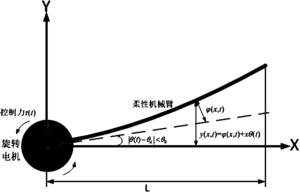

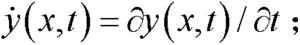
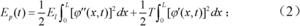
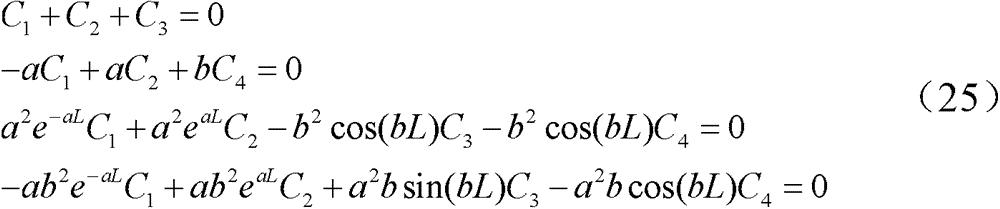

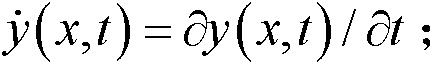
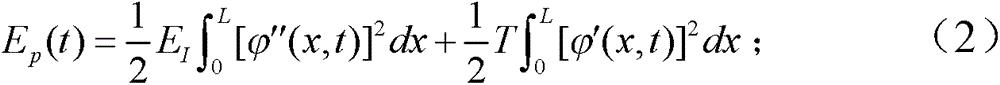








 苏公网安备 32041202001399号
苏公网安备 32041202001399号



 loading...
loading...