【中国发明,中国发明授权】具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法
无权-未缴年费 中国
- 申请号:
- CN201410494011.X
- 专利权人:
- 哈尔滨工业大学
- 授权公告日/公开日:
- 2016.08.24
- 专利有效期:
- 2014.09.24-2034.09.24
- 技术分类:
- B25:手动工具;轻便机动工具;手动器械的手柄;车间设备;机械手
- 转化方式:
- 转让
- 价值度指数:
-
- 53.0分
- 价格:
- 面议
- 专利信息&法律状态
- 专利自评
- 专利技术文档
- 价值度指数
- 发明人阵容
 著录项
著录项
- 申请号
- CN201410494011.X
- 申请日
- 20140924
- 公开/公告号
- CN104400783A
- 公开/公告日
- 20150311
- 申请/专利权人
- [哈尔滨工业大学]
- 发明/设计人
- [吴伟国, 侯月阳]
- 主分类号
- B25J9/16
- IPC分类号
- C12N 9/0008(2013.01) C12N 9/16
- CPC分类号
- C12N 9/0008(2013.01) C12N 9/16(2013.01)
- 分案申请地址
- 国省代码
- 黑龙江(23)
- 颁证日
- G06T1/00
- 代理人
- [杨立超]
 摘要
摘要
具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法,属于机器人应用控制领域。本发明为了实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制,以减小挠性驱动关节控制误差、提高系统频响。本发明提出基于粘弹性动力学模型补偿的控制策略并设计了挠性驱动单元控制器,根据钢丝绳弹性变形公式设计前馈控制器,通过电机角度估计值公式设计反馈控制器,该设计方法适用于机器人关节用挠性驱动单元的控制器设计;搭建挠性驱动单元控制系统硬件,通过关节编码器进行关节位置反馈,利用电机位置估计值进行电机位置反馈,从而实现驱动单元控制系统位置全闭环。与经典PID控制方法相比,可显著提高伺服控制精度,减小跟踪误差,并提高系统频响。
 法律状态
法律状态
| 法律状态公告日 | 20240920 |
| 法律状态 | 专利权的终止 |
| 法律状态信息 | 未缴年费专利权终止 IPC(主分类):B25J 9/16 专利号:ZL201410494011X 申请日:20140924 授权公告日:20160824 终止日期: |
| 法律状态公告日 | 20160824 |
| 法律状态 | 授权 |
| 法律状态信息 | 授权 |
| 法律状态公告日 | 20150408 |
| 法律状态 | 实质审查的生效 |
| 法律状态信息 | 实质审查的生效 IPC(主分类):B25J 9/16 申请日:20140924 |
| 法律状态公告日 | 20150311 |
| 法律状态 | 公开 |
| 法律状态信息 | 公开 |
 权利要求
权利要求
权利要求数量(4)
独立权利要求数量(1)
1.一种具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法,所述控制 方法用于控制一种绳驱动、动滑轮增力、带有张力传感器、关节编码器的机器人关节用挠 性驱动单元,以实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制;其特征在于: 所述控制方法的实现过程为:
步骤一、推导挠性驱动单元粘弹性动力学模型,以获得驱动单元粘弹性动力学模型与 钢丝绳弹性变形公式;
步骤二、对关节速度与加速度进行前馈:基于粘弹性动力学模型补偿的控制策略并设 计挠性驱动单元控制器,根据钢丝绳弹性变形公式设计前馈控制器,通过电机角度估计值 公式设计反馈控制器;
步骤三、进行关节全闭环反馈控制;通过关节编码器进行关节位置反馈,利用电机位 置估计值进行电机位置反馈,从而实现驱动单元控制系统位置全闭环。
2.根据权利要求1所述的具有张力和关节位置反馈的机器人关节用挠性驱动单元控制 方法,其特征在于:所述控制方法的具体实现过程为:
步骤一、推导挠性驱动单元粘弹性动力学模型,以获得驱动单元粘弹性动力学模型与 钢丝绳弹性变形公式,其过程为:
减速器输出轴缠绕钢丝绳钢丝绳张力表示如下:
其中,下标i=1,2;
其它参数的含义如下:
k i表示钢丝绳L i的等效刚度(i=1,2,3,4),k i=EA/L i
E表示钢丝绳杨氏模量,A表示钢丝绳横截面积,x i表示钢丝绳L i的位移,r 1表示减速 器输出轴半径,θ 1表示减速器输出轴角度;c i表示钢丝绳L i的等效阻尼,c i=f 1A/L i,f 1表示 钢丝绳粘性系数;F i,initial表示钢丝绳L i预紧力;
求解上式,取初位移与初速度均为零,得到减速器输出轴缠绕钢丝绳位移为:
其中,下标i=1,2;由动滑轮组增力减速原理有:
由于减速器端钢丝绳张力未知,而关节端钢丝绳张力由张力传感器测得,用关节端张 力代替减速器端钢丝绳张力,已知F 1,F 2,F 3,F 4与F′ 1,F′ 2,F′ 3,F′ 4分别互为反力,则减速 器输出轴缠绕钢丝绳位移为如下形式:
其中,下标i=1,2,j=3,4,联立公式(9)和(10),得到关节输出轴缠绕钢丝绳位移为:
其中,下标i,j值同上;假定挠性驱动单元关节两侧钢丝绳的拉伸和放松量相同,得到 关节两侧钢丝绳变形约束条件:
x 3+x 4=2r 2θ 2 (13)
r 2表示关节输出轴半径,θ 2表示关节输出轴角度;
联立公式(11)和(13),得到基于粘弹性动力学的挠性驱动单元关节角公式:
当忽略钢丝绳伸长量与单元速度关系时阻尼系数为零,由式(7)求得关节输出轴缠绕 钢丝绳位移为:
其中,下标i=1,2,j=3,4;推导出钢丝绳弹性变形为:
△x j=x j-r 2θ 2 (16)
其中,下标i,j值同上;联立公式(13)和(15),得到挠性驱动单元关节角公式如下:
步骤二、对关节速度与加速度进行前馈;
根据钢丝绳张力公式(7)可方便求出任意时刻的钢丝绳张力F,该值包含钢丝绳预紧力、 摩擦力和钢丝绳伸长后的回复力,联立公式(15)和(16)可求出关节两侧钢丝绳弹性变形:
其中,下标i,j值同公式(16);由于假定钢丝绳始终处于拉紧状态,因此,△x 3和△x 4 均大于零,前馈计算需要的钢丝绳弹性伸长对应关节转动方向,该伸长值大于关节转动反 方向的伸长值,那么,在前馈计算首先要根据关节旋转方向判断前馈要使用的钢丝绳弹性 伸长值,判断如下:如果θ 2>0,即关节逆时针转动,那么下标j=3;否则,j=4;计算前馈 速度与加速度公式如下:
式中: 表示电机前馈角速度, 表示电机前馈角加速度,△T表示伺服周期,
根据上式可实时修改速度与加速度前馈系数,该系数由当前参考位置和参考速度与前 馈的速度与加速度求得:
表示电机期望速度, 表示电机期望加速度,K vff表示关节前馈速度系数,K aff表 示关节前馈加速度系数;
步骤三、进行关节全闭环反馈控制;
进行关节全闭环控制,设计反馈控制器,需要的反馈物理量为关节编码器角度值和张 力传感器值,由公式(17)可求出由θ 2、r、F 3和F 4表示的电机角度估计值,如下:
式中,θ 2,r表示关节实际角度; 表示电机角度估计值;
通过粘弹性动力学模型,根据关节两侧张力值和关节角度值进行相关运算求出电机实 际角度,在此并未直接读取电机编码器角度值进行反馈,将粘弹性动力学模型引入到反馈 控制回路;
电机角度估计值与电机参考值做比较,两者的误差反馈补偿公式如下:
e1表示角度误差反馈,K P2表示电机位置误差反馈比例系数,θ 0,e表示电机期望角度值, 表示电机角度估计值;
将位置误差补偿到指令电机期望角度值中,使电机参考轨迹根据电机实际角度变化趋 势进行实时修改,实现反馈控制,K P2受到电机实际速度和钢丝绳张力因素的影响,手动调 节K P2要使误差在允许范围内;
将电机角度估计值进行差分计算,得到基于粘弹性动力学模型的电机速度估计值,将 该估计值与电机实际速度做差,则两者的误差反馈补偿公式如下:
式中,e 2表示速度误差反馈,K D2表示电机速度误差反馈比例系数, 表示电机速度估 计值, 表示电机实际速度;
K D2受到钢丝绳张力和电机实际速度的影响,K P2、K D2根据钢丝绳张力、电机实际速度 进行实时修改,具体调节方法为:获得比例系数K P2、微分系数K D2与钢丝绳张力、电机实 际速度的对应关系作为数据表存入运动控制卡内存,在挠性驱动单元系统运行时根据采集 的钢丝绳张力、电机实际速度调用该数据表从而进行参数的实时修改。
3.根据权利要求2所述的一种具有张力和关节位置反馈的机器人关节用挠性驱动单元 控制方法,其特征在于:根据所述方法设计的控制器通过上位机轨迹生成器生成关节角及 角速度序列,发送至运动控制卡进行伺服插值计算,伺服插值计算之前,先进行关节角及 角速度的反馈,该反馈根据挠性驱动单元粘弹性动力学推导的关节角公式进行四则运算及 微分,得到的关节角度及角速度估计值用于对关节参考角度与角速度进行反馈;在伺服插 值计算之后,进行速度和加速度的前馈,前馈系数根据关节角与钢丝绳张力得到的关节端 两侧钢丝绳变形量进行计算得到。
4.权利要求1、2或3所述方法中的挠性驱动单元为FDU-II型挠性驱动单元,其特征 在于:FDU-II型挠性驱动单元的频响测试过程为:输入频率序列f为从f 0开始,以f d为等 差项递增,直到f n,共有S个频率序列。采用变幅值变频率余弦函数作为输入函数,令A 0 为最大幅值,A 1为变化的幅值向量,表示如下:
参考输入函数如下:
其中,下标i=12...S;上述函数为FDU-II型挠性驱动单元频响测试的输入函数。
1.一种具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法,所述控制方法用于控制一种绳驱动、动滑轮增力、带有张力传感器、关节编码器的机器人关节用挠性驱动单元,以实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制;其特征在于:所述控制方法的实现过程为:
步骤一、推导挠性驱动单元粘弹性动力学模型,以获得驱动单元粘弹性动力学模型与钢丝绳弹性变形公式;
步骤二、对关节速度与加速度进行前馈:基于粘弹性动力学模型补偿的控制策略并设计挠性驱动单元控制器,根据钢丝绳弹性变形公式设计前馈控制器,通过电机角度估计值公式设计反馈控制器;
步骤三、进行关节全闭环反馈控制;通过关节编码器进行关节位置反馈,利用电机位置估计值进行电机位置反馈,从而实现驱动单元控制系统位置全闭环。
2.根据权利要求1所述的具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法,其特征在于:所述控制方法的具体实现过程为:
步骤一、推导挠性驱动单元粘弹性动力学模型,以获得驱动单元粘弹性动力学模型与钢丝绳弹性变形公式,其过程为:
减速器输出轴缠绕钢丝绳钢丝绳张力表示如下:
F i = - k i ( x i - r 1 θ 1 ) - c i ( x . i - r 1 θ . 1 ) + F i , initial - - - ( 7 ) ]]>
其中,下标i=1,2;
其它参数的含义如下:
ki表示钢丝绳Li的等效刚度(i=1,2,3,4),ki=EA/Li
E表示钢丝绳杨氏模量,A表示钢丝绳横截面积,xi表示钢丝绳Li的位移,r1表示减速器输出轴半径,θ1表示减速器输出轴角度;ci表示钢丝绳Li的等效阻尼,ci=f1A/Li,f1表示钢丝绳粘性系数;Fi,initial表示钢丝绳Li预紧力;
求解上式,取初位移与初速度均为零,得到减速器输出轴缠绕钢丝绳位移为:
x i = e - k i c i t [ ( r 1 θ 1 + F i , initial k i ) ( e k i c i t - 1 ) - 1 c i ∫ t 0 t F i e k i c i t dt ] - - - ( 8 ) ]]>
其中,下标i=1,2;由动滑轮组增力减速原理有:
F 3 ′ = 4 F 1 ′ F 4 ′ = 4 F 2 ′ x 3 = 1 4 x 1 x 4 = 1 4 x 2 - - - ( 9 ) ]]>
由于减速器端钢丝绳张力未知,而关节端钢丝绳张力由张力传感器测得,用关节端张力代替减速器端钢丝绳张力,已知F1,F2,F3,F4与F′1,F′2,F′3,F′4分别互为反力,则减速器输出轴缠绕钢丝绳位移为如下形式:
x i = e - k i c i t [ ( r 1 θ 1 + F j , initial 4 k j ) ( e k i c i t - 1 ) - 1 4 c i ∫ t 0 t F j e k i c i t dt ] - - - ( 10 ) ]]>
其中,下标i=1,2,j=3,4,联立公式(9)和(10),得到关节输出轴缠绕钢丝绳位移为:
x j = 1 4 e - k i c i t [ ( r 1 θ 1 + F j , initial 4 k i ) ( e k i c i t - 1 ) - 1 4 c i ∫ t 0 t F j e k i c i t dt ] - - - ( 11 ) ]]>
其中,下标i,j值同上;假定挠性驱动单元关节两侧钢丝绳的拉伸和放松量相同,得到关节两侧钢丝绳变形约束条件:
x3+x4=2r2θ2 (13)
r2表示关节输出轴半径,θ2表示关节输出轴角度;
联立公式(11)和(13),得到基于粘弹性动力学的挠性驱动单元关节角公式:
θ 2 ( θ 1 , F 3 , F 4 , t ) = 1 8 r 2 e k 1 c 1 t [ ( r 1 θ 1 + F 3 , initial 4 k 1 ) ( e k 1 c 1 t - 1 ) - 1 4 c 1 ∫ t 0 t F 3 e k 1 c 1 t dt ] + e - k 2 c 2 t [ ( r 1 θ 1 + F 4 , initial 4 k 4 ) ( e k 2 c 2 t - 1 ) - 1 4 c 2 ∫ c 2 t F 4 e k 2 c 2 t dt ] - - - ( 14 ) ]]>
当忽略钢丝绳伸长量与单元速度关系时阻尼系数为零,由式(7)求得关节输出轴缠绕钢丝绳位移为:
x j = 1 4 ( r 1 θ 1 + F j , initial - F j 4 k i ) - - - ( 15 ) ]]>
其中,下标i=1,2,j=3,4;推导出钢丝绳弹性变形为:
△xj=xj-r2θ2 (16)
其中,下标i,j值同上;联立公式(13)和(15),得到挠性驱动单元关节角公式如下:
θ 2 ( θ 1 , F 3 , F 4 ) = 1 8 r 2 ( 2 r 1 θ 1 + F 3 , initial - F 3 4 k 1 + F 4 , initial - F 4 4 k 2 ) - - - ( 17 ) ]]>
步骤二、对关节速度与加速度进行前馈;
根据钢丝绳张力公式(7)可方便求出任意时刻的钢丝绳张力F,该值包含钢丝绳预紧力、摩擦力和钢丝绳伸长后的回复力,联立公式(15)和(16)可求出关节两侧钢丝绳弹性变形:
Δx j = 1 4 ( r 1 θ 1 + F j , initial - F j 4 k i ) - r 2 θ 2 - - - ( 18 ) ]]>
其中,下标i,j值同公式(16);由于假定钢丝绳始终处于拉紧状态,因此,△x3和△x4均大于零,前馈计算需要的钢丝绳弹性伸长对应关节转动方向,该伸长值大于关节转动反方向的伸长值,那么,在前馈计算首先要根据关节旋转方向判断前馈要使用的钢丝绳弹性伸长值,判断如下:如果θ2>0,即关节逆时针转动,那么下标j=3;否则,j=4;计算前馈速度与加速度公式如下:
Δ θ . 0 = i m i r Δ x j / r 1 ΔT Δ θ . . 0 = Δ θ . 0 / ΔT - - - ( 19 ) ]]>
式中:表示电机前馈角速度,表示电机前馈角加速度,△T表示伺服周期,
根据上式可实时修改速度与加速度前馈系数,该系数由当前参考位置和参考速度与前馈的速度与加速度求得:
K vff = Δ θ . 0 / θ . 0 , e K aff = Δ θ . . 0 / θ . . 0 , e - - - ( 20 ) ]]>
表示电机期望速度,表示电机期望加速度,Kvff表示关节前馈速度系数,Kaff表示关节前馈加速度系数;
步骤三、进行关节全闭环反馈控制;
进行关节全闭环控制,设计反馈控制器,需要的反馈物理量为关节编码器角度值和张力传感器值,由公式(17)可求出由θ2、r、F3和F4表示的电机角度估计值,如下:
θ ^ 0 ( F 3 , F 4 , θ 2 , r ) = i r 2 r 1 ( 8 r 2 θ 2 , r - F 3 , initial - F 3 4 k 1 - F 4 , initial - F 4 4 k 2 ) - - - ( 21 ) ]]>
式中,θ2,r表示关节实际角度;表示电机角度估计值;
通过粘弹性动力学模型,根据关节两侧张力值和关节角度值进行相关运算求出电机实际角度,在此并未直接读取电机编码器角度值进行反馈,将粘弹性动力学模型引入到反馈控制回路;
电机角度估计值与电机参考值做比较,两者的误差反馈补偿公式如下:
e 1 = K P 2 ( θ ^ 0 - θ 0 , e ) - - - ( 22 ) ]]>
e1表示角度误差反馈,KP2表示电机位置误差反馈比例系数,θ0,e表示电机期望角度值,表示电机角度估计值;
将位置误差补偿到指令电机期望角度值中,使电机参考轨迹根据电机实际角度变化趋势进行实时修改,实现反馈控制,KP2受到电机实际速度和钢丝绳张力因素的影响,手动调节KP2要使误差在允许范围内;
将电机角度估计值进行差分计算,得到基于粘弹性动力学模型的电机速度估计值,将该估计值与电机实际速度做差,则两者的误差反馈补偿公式如下:
e 2 = K D 2 ( θ ^ . 0 - θ . 0 , r ) - - - ( 23 ) ]]>
式中,e2表示速度误差反馈,KD2表示电机速度误差反馈比例系数,表示电机速度估计值,表示电机实际速度;
KD2受到钢丝绳张力和电机实际速度的影响,KP2、KD2根据钢丝绳张力、电机实际速度进行实时修改,具体调节方法为:获得比例系数KP2、微分系数KD2与钢丝绳张力、电机实际速度的对应关系作为数据表存入运动控制卡内存,在挠性驱动单元系统运行时根据采集的钢丝绳张力、电机实际速度调用该数据表从而进行参数的实时修改。
3.根据权利要求2所述的一种具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法,其特征在于:根据所述方法设计的控制器通过上位机轨迹生成器生成关节角及角速度序列,发送至运动控制卡进行伺服插值计算,伺服插值计算之前,先进行关节角及角速度的反馈,该反馈根据挠性驱动单元粘弹性动力学推导的关节角公式进行四则运算及微分,得到的关节角度及角速度估计值用于对关节参考角度与角速度进行反馈;在伺服插值计算之后,进行速度和加速度的前馈,前馈系数根据关节角与钢丝绳张力得到的关节端两侧钢丝绳变形量进行计算得到。
4.权利要求1、2或3所述方法中的挠性驱动单元为FDU-II型挠性驱动单元,其特征在于:FDU-II型挠性驱动单元的频响测试过程为:输入频率序列f为从f0开始,以fd为等差项递增,直到fn,共有S个频率序列。采用变幅值变频率余弦函数作为输入函数,令A0为最大幅值,A1为变化的幅值向量,表示如下:
A 1 = A 0 × 1 S - 1 S . . . 1 S 1.5 ]]>
参考输入函数如下:
P i = P i - 1 + A 1 i [ cos ( 2 π T i t i ) - 1 ] ]]>
其中,下标i=12...S;上述函数为FDU-II型挠性驱动单元频响测试的输入函数。
 说明书
说明书
技术领域
本发明涉及一种机器人关节用挠性驱动单元控制方法,具体涉及一种适用于绳驱动、动滑轮增力、具有张力和关节位置反馈的机器人关节用挠性驱动单元的控制方法,属于机器人应用控制领域。
背景技术
相比刚性驱动,钢丝绳柔性驱动能够吸收震动,减缓冲击,但由于其导致关节回差较大、且有明显滞后,采用经典PID控制方法效果欠佳。经文献检索发现中国专利公告号为CN101863034B,专利号为201010210888.3,名称为由滑轮组与钢丝绳牵引驱动的机器人关节用挠性驱动单元是一种绳驱动关节挠性驱动单元,但没有给出控制方法。申请号为201410257786.5的一种绳驱动、动滑轮增力、带有张力传感器、关节编码器的机器人关节用挠性驱动单元没有给出有效的控制方法,无法实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制,存在控制误差大的问题。
发明内容
本发明的目的是为一种绳驱动、动滑轮增力、带有张力传感器、关节编码器的机器人关节用挠性驱动单元(申请号:201410257786.5)提供有效的控制方法,实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制,以减小挠性驱动关节控制误差、提高系统频响。
本发明为解决上述技术问题采取的技术方案是:
一种具有张力和关节位置反馈的机器人关节用挠性驱动单元控制方法,所述控制方法用于控制一种绳驱动、动滑轮增力、带有张力传感器、关节编码器的机器人关节用挠性驱动单元,以实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制;所述控制方法的实现过程为:
步骤一、推导挠性驱动单元粘弹性动力学模型,以获得驱动单元粘弹性动力学模型与钢丝绳弹性变形公式;
步骤二、对关节速度与加速度进行前馈:基于粘弹性动力学模型补偿的控制策略并设计挠性驱动单元控制器,根据钢丝绳弹性变形公式设计前馈控制器,通过电机角度估计值公式设计反馈控制器;
步骤三、进行关节全闭环反馈控制;通过关节编码器进行关节位置反馈,利用电机位置估计值进行电机位置反馈,从而实现驱动单元控制系统位置全闭环。
所述控制方法的具体实现过程为:
步骤一、推导挠性驱动单元粘弹性动力学模型,以获得驱动单元粘弹性动力学模型与钢丝绳弹性变形公式,其过程为:
减速器输出轴缠绕钢丝绳钢丝绳张力表示如下:
F i = - k i ( x i - r 1 θ 1 ) - c i ( x . i - r 1 θ . 1 ) + F i , initial - - - ( 7 ) ]]>
其中,下标i=1,2;
其它参数的含义如下:
ki表示钢丝绳Li的等效刚度(i=1,2,3,4),ki=EA/Li
E表示钢丝绳杨氏模量,A表示钢丝绳横截面积,xi表示钢丝绳Li的位移,r1表示减速器输出轴半径,θ1表示减速器输出轴角度;ci表示钢丝绳Li的等效阻尼,ci=f1A/Li,f1表示钢丝绳粘性系数;Fi,initial表示钢丝绳Li预紧力;
求解上式,取初位移与初速度均为零,得到减速器输出轴缠绕钢丝绳位移为:
x i = e - k i c i t [ ( r 1 θ 1 + F i , initial k i ) ( e k i c i t - 1 ) - 1 c i ∫ t 0 t F i e k i c i t dt ] - - - ( 8 ) ]]>
其中,下标i=1,2;由动滑轮组增力减速原理有:
F 3 ′ = 4 F 1 ′ F 4 ′ = 4 F 2 ′ x 3 = 1 4 x 1 x 4 = 1 4 x 2 - - - ( 9 ) ]]>
由于减速器端钢丝绳张力未知,而关节端钢丝绳张力由张力传感器测得,用关节端张力代替减速器端钢丝绳张力,已知F1,F2,F3,F4与F′1,F′2,F′3,F′4分别互为反力,则减速器输出轴缠绕钢丝绳位移为如下形式:
x i = e - k i c i t [ ( r 1 θ 1 + F j , initial 4 k j ) ( e k i c i t - 1 ) - 1 4 c i ∫ t 0 t F j e k i c i t dt ] - - - ( 10 ) ]]>
其中,下标i=1,2,j=3,4,联立公式(9)和(10),得到关节输出轴缠绕钢丝绳位移为:
x j = 1 4 e - k i c i t [ ( r 1 θ 1 F j , initial 4 k i ) ( e k i c i t - 1 ) - 1 4 c i ∫ t 0 t F j e k i c i t dt ] - - - ( 11 ) ]]>
其中,下标i,j值同上;假定挠性驱动单元关节两侧钢丝绳的拉伸和放松量相同,得到关节两侧钢丝绳变形约束条件:
x3+x4=2r2θ2 (13)
r2表示关节输出轴半径,θ2表示关节输出轴角度;
联立公式(11)和(13),得到基于粘弹性动力学的挠性驱动单元关节角公式:
θ 2 ( θ 1 , F 3 , F 4 , t ) = 1 8 r 2 e k 1 c 1 t [ ( r 1 θ 1 + F 3 , initial 4 k 1 ) ( e k 1 c 1 t - 1 ) - 1 4 c 1 ∫ t 0 t F 3 e k 1 c 1 t dt ] + e - k 2 c 2 t [ ( r 1 θ 1 + F 4 , initial 4 k 4 ) ( e k 2 c 2 t - 1 ) - 1 4 c 2 ∫ c 2 t F 4 e k 2 c 2 t dt ] - - - ( 14 ) ]]>
当忽略钢丝绳伸长量与单元速度关系时阻尼系数为零,由式(7)求得关节输出轴缠绕钢丝绳位移为:
x j = 1 4 ( r 1 θ 1 + F j , initial - F j 4 k i ) - - - ( 15 ) ]]>
其中,下标i=1,2,j=3,4;推导出钢丝绳弹性变形为:
△xj=xj-r2θ2 (16)
其中,下标i,j值同上;联立公式(13)和(15),得到挠性驱动单元关节角公式如下:
θ 2 ( θ 1 , F 3 , F 4 ) = 1 8 r 2 ( 2 r 1 θ 1 + F 3 , initial - F 3 4 k 1 + F 4 , initial - F 4 4 k 2 ) - - - ( 17 ) ]]>
步骤二、对关节速度与加速度进行前馈;
根据钢丝绳张力公式(7)可方便求出任意时刻的钢丝绳张力F,该值包含钢丝绳预紧力、摩擦力和钢丝绳伸长后的回复力,联立公式(15)和(16)可求出关节两侧钢丝绳弹性变形:
Δx j = 1 4 ( r 1 θ 1 + F j , initial - F j 4 k i ) - r 2 θ 2 - - - ( 18 ) ]]>
其中,下标i,j值同公式(16);由于假定钢丝绳始终处于拉紧状态,因此,△x3和△x4均大于零,前馈计算需要的钢丝绳弹性伸长对应关节转动方向,该伸长值大于关节转动反方向的伸长值,那么,在前馈计算首先要根据关节旋转方向判断前馈要使用的钢丝绳弹性伸长值,判断如下:如果θ2>0,即关节逆时针转动,那么下标j=3;否则,j=4;计算前馈速度与加速度公式如下:
Δ θ . 0 = i m i r Δ x j / r 1 ΔT Δ θ . . 0 = Δ θ . 0 / ΔT - - - ( 19 ) ]]>
式中:表示电机前馈角速度,表示电机前馈角加速度,△T表示伺服周期,
根据上式可实时修改速度与加速度前馈系数,该系数由当前参考位置和参考速度与前馈的速度与加速度求得:
K vff = Δ θ . 0 / θ . 0 , e K aff = Δ θ . . 0 / θ . . 0 , e - - - ( 20 ) ]]>
表示电机期望速度,表示电机期望加速度,Kvff表示关节前馈速度系数,Kaff表示关节前馈加速度系数;
步骤三、进行关节全闭环反馈控制;
进行关节全闭环控制,设计反馈控制器,需要的反馈物理量为关节编码器角度值和张力传感器值,由公式(17)可求出由θ2、r、F3和F4表示的电机角度估计值,如下:
θ ^ 0 ( F 3 , F 4 , θ 2 , r ) = i r 2 r 1 ( 8 r 2 θ 2 , r - F 3 , initial - F 3 4 k 1 - F 4 , initial - F 4 4 k 2 ) - - - ( 21 ) ]]>
式中,θ2,r表示关节实际角度;表示电机角度估计值;
通过粘弹性动力学模型(公式14),根据关节两侧张力值和关节角度值进行相关运算求出电机实际角度,在此并未直接读取电机编码器角度值进行反馈,将粘弹性动力学模型引入到反馈控制回路;
电机角度估计值与电机参考值做比较,两者(“电机角度估计值”与“电机期望角值”)的误差反馈补偿公式如下:
e 1 = K P 2 ( θ ^ 0 - θ 0 , e ) - - - ( 22 ) ]]>
e1表示角度误差反馈,KP2表示电机位置误差反馈比例系数,θ0,e表示电机期望角度值,表示电机角度估计值;
将位置误差补偿到指令电机期望角度值中,使电机参考轨迹根据电机实际角度变化趋势进行实时修改,实现反馈控制,KP2受到电机实际速度和钢丝绳张力因素的影响,手动调节KP2要使误差在允许范围内;
将电机角度估计值进行差分计算,得到基于粘弹性动力学模型的电机速度估计值,将该估计值与电机实际速度做差,则两者的误差反馈补偿公式如下:
e 2 = K D 2 ( θ ^ . 0 - θ . 0 , r ) - - - ( 23 ) ]]>
式中,e2表示速度误差反馈,KD2表示电机速度误差反馈比例系数,表示电机速度估计值,表示电机实际速度;
KD2受到钢丝绳张力和电机实际速度的影响,KP2、KD2根据钢丝绳张力、电机实际速度进行实时修改,具体调节方法为:获得比例系数KP2、微分系数KD2(电机速度误差反馈比例系数)与钢丝绳张力、电机实际速度的对应关系作为数据表存入运动控制卡内存,在挠性驱动单元系统运行时根据采集的钢丝绳张力、电机实际速度调用该数据表从而进行参数的实时修改。
根据所述方法设计的控制器(是指图4所示控制器)通过上位机轨迹生成器生成关节角及角速度序列,发送至运动控制卡进行伺服插值计算,伺服插值计算之前,先进行关节角及角速度的反馈,该反馈根据挠性驱动单元粘弹性动力学推导的关节角公式进行四则运算及微分,得到的关节角度及角速度估计值用于对关节参考角度与角速度进行反馈;在伺服插值计算之后,进行速度和加速度的前馈,前馈系数根据关节角与钢丝绳张力得到的关节端两侧钢丝绳变形量进行计算得到。
上述方法中的挠性驱动单元为FDU-II型挠性驱动单元,所述FDU-II型挠性驱动单元的频响测试过程为:输入频率序列f为从f0开始,以fd为等差项递增,直到fn,共有S个频率序列。采用变幅值变频率余弦函数作为输入函数,令A0为最大幅值,A1为变化的幅值向量,表示如下:
A 1 = A 0 × 1 S - 1 S . . . 1 S 1.5 ]]>
参考输入函数如下:
P i = P i - 1 + A 1 i [ cos ( 2 π T i t i ) - 1 ] ]]>
其中,下标i=12...S;上述函数为FDU-II型挠性驱动单元频响测试的输入函数。
本发明的有益效果是:
本发明是为一种机器人关节用挠性驱动单元提供一种可实现张力反馈、关节全闭环控制的控制方法,本发明提出基于粘弹性动力学模型补偿的控制策略并设计了挠性驱动单元控制器,根据钢丝绳弹性变形公式设计了前馈控制器,通过电机角度估计值公式设计了反馈控制器,该设计方法适用于机器人关节用挠性驱动单元的控制器设计,并可显著提高伺服控制精度,减小跟踪误差,并提高系统频响;搭建了挠性驱动单元控制系统硬件,通过关节编码器进行关节位置反馈,利用电机位置估计值进行电机位置反馈,从而实现了驱动单元控制系统位置全闭环。本控制方法优点是算法简单有效,可根据钢丝绳张力对单元进行速度与加速度前馈,并实现机器人关节的全闭环控制,与经典PID控制方法相比,可显著提高伺服控制精度,减小跟踪误差,并提高系统频响。
本发明方法实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制,而且减小了挠性驱动关节控制误差、提高系统频响。本发明提出基于粘弹性动力学模型补偿的控制策略并设计了挠性驱动单元控制器,根据钢丝绳弹性变形公式设计了前馈控制器,通过电机角度估计值公式设计了反馈控制器,该设计方法适用于机器人关节用挠性驱动单元的控制器设计;搭建了挠性驱动单元控制系统硬件,通过关节编码器进行关节位置反馈,利用电机位置估计值进行电机位置反馈,从而实现了驱动单元控制系统位置全闭环。
本发明方法用于实现机器人关节用挠性驱动装置张力反馈和关节全闭环控制。本发明提出基于粘弹性动力学模型补偿的控制策略并设计挠性驱动单元控制器,根据钢丝绳弹性变形公式设计了前馈控制器,通过电机角度估计值公式设计了反馈控制器;搭建挠性驱动单元控制系统硬件,通过关节编码器进行关节位置反馈,利用电机位置估计值进行电机位置反馈,从而实现驱动单元控制系统位置全闭环。
附图说明
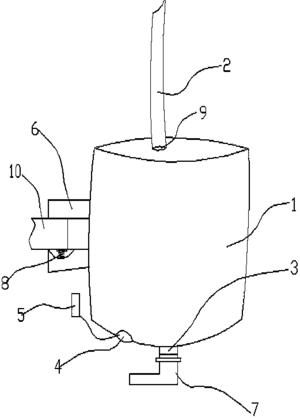
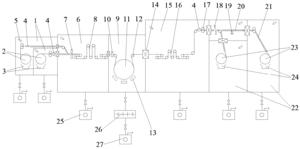
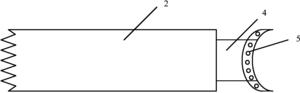
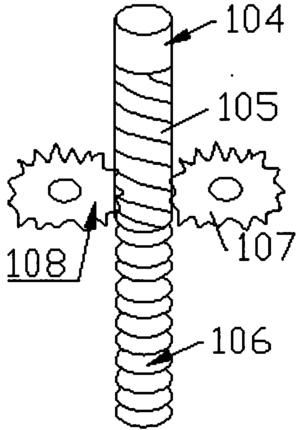
图1是本发明的被控对象虚拟样机图(即申请号为201410257786.5的一种绳驱动、动滑轮增力、带有张力传感器、关节编码器的机器人关节用挠性驱动单元),图2是本发明的被控对象机构原理图(挠性驱动单元机构原理),图3是本发明的被控对象动力学模型示意图(挠性驱动单元动力学模型),图4是本发明设计的控制器框图及其原理图,其中,a)为控制器框图,b)为控制器原理图;图5为本发明应用实例控制系统硬件系统照片,其中,a)是本发明应用实例1控制系统硬件系统照片(图中:1-上位机、2-砝码、3-驱动单元、4-加载装置、5-运动控制卡及A/D、6-驱动器、7-直流开关电源),b)是本发明应用实例2控制系统硬件系统照片;图6是本发明控制系统框图;图7-图10是本发明频响测试结果图,其分别是关节理论与实际转角、关节跟踪误差、关节转角幅值峰值点频率、幅频特性,图7为关节理论与实际转角对比图,图8为关节跟踪误差图,图9为关节转角幅值峰值点频率图,图10是幅频特性对比图;图11是关节相位图。
具体实施方式
具体实施方式五:本专利应用实例2为带有挠性驱动单元的双足机器人系统,其控制系统硬件照片如图5b)所示,挠性驱动单元采用权利要求一所述的控制方法,进行双足机器人步行实验,单腿迈步周期5s,单脚支撑期3s,双脚支撑期2s,复步长260mm,机器人在四个完整步行周期(不包括步行初始阶段半步和步行完成阶段半步)内步行距离1040mm,步行时间40s,达到约0.1km/h的步速,挠性驱动单元的关节极限环(图11中的大环)呈现周期性循环状态,表明机器人在迈复步的步行过程中处于稳定状态。
本发明方法中所有参数或变量的含义参现表一:
表一 本发明控制方法说明所需变量表
 价值度评估
价值度评估
技术价值
经济价值
法律价值
0 0 053.0分
0 50 75 100专利价值度是通过科学的评估模
型对专利价值进行量化的结果,
基于专利大数据针对专利总体特
征指标利用计算机自动化技术对
待评估专利进行高效、智能化的
分析,从技术、经济和法律价值
三个层面构建专利价值评估体
系,可以有效提升专利价值评估
的质量和效率。
总评:53.0分
该专利价值中等 (仅供参考)
本专利文献中包含【1 个技术分类】,从一定程度上而言上述指标的数值越大可以反映出所述专利的技术保护及应用范围越广。 【专利权的维持时间10 年】专利权的维持时间越长,其价值对于权利人而言越高。
技术价值 30.0
该指标主要从专利申请的著录信息、法律事件等内容中挖掘其技术价值,专利类型、独立权利要求数量、无效请求次数等内容均可反映出专利的技术性价值。 技术创新是专利申请的核心,若您需要进行技术借鉴或寻找可合作的项目,推荐您重点关注该指标。
部分指标包括:
授权周期(发明)
23 个月独立权利要求数量
0 个从属权利要求数量
0 个说明书页数
9 页实施例个数
0 个发明人数量
2 个被引用次数
0 次引用文献数量
0 个优先权个数
0 个技术分类数量
1 个无效请求次数
0 个分案子案个数
0 个同族专利数
0 个专利获奖情况
无保密专利的解密
否经济价值 7.0
该指标主要指示了专利技术在商品化、产业化及市场化过程中可能带来的预期利益。 专利技术只有转化成生产力才能体现其经济价值,专利技术的许可、转让、质押次数等指标均是其经济价值的表征。 因此,若您希望找到行业内的运用广泛的热点专利技术及侵权诉讼中的涉案专利,推荐您重点关注该指标。
部分指标包括:
申请人数量
1申请人类型
院校许可备案
0 次权利质押
0 次权利转移
0 个海关备案
否法律价值 16.0
该指标主要从专利权的稳定性角度评议其价值。专利权是一种垄断权,但其在法律保护的期间和范围内才有效。 专利权的存续时间、当前的法律状态可反映出其法律价值。故而,若您准备找寻权属稳定且专利权人非常重视的专利技术,推荐您关注该指标。
部分指标包括:
存活期/维持时间
10法律状态
无权-未缴年费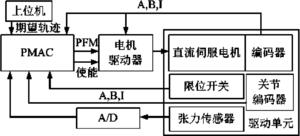








 苏公网安备 32041202001399号
苏公网安备 32041202001399号



 loading...
loading...