【中国发明,中国发明授权】基于近似模型多步优化的清洁机器人最优路径规划方法
有权-审定授权 中国
- 申请号:
- CN201810385471.7
- 专利权人:
- 常熟理工学院
- 授权公告日/公开日:
- 2019.11.08
- 专利有效期:
- 2018.04.26-2038.04.26
- 技术分类:
- G05:控制;调节
- 转化方式:
- 转让
- 价值度指数:
-
- 55.0分
- 价格:
- 面议
- 专利信息&法律状态
- 专利自评
- 专利技术文档
- 价值度指数
- 发明人阵容
 著录项
著录项
- 申请号
- CN201810385471.7
- 申请日
- 20180426
- 公开/公告号
- CN108762249A
- 公开/公告日
- 20181106
- 申请/专利权人
- [常熟理工学院]
- 发明/设计人
- [钟珊, 龚声蓉, 董瑞志, 姚宇峰, 马帅]
- 主分类号
- G05D1/02
- IPC分类号
- C12N 9/0008(2013.01) C12N 9/16
- CPC分类号
- C12N 9/0008(2013.01) C12N 9/16(2013.01)
- 分案申请地址
- 国省代码
- 江苏(32)
- 颁证日
- G06T1/00
- 代理人
- [张俊范]
 摘要
摘要
本发明公开了一种基于近似模型多步优化的清洁机器人最优路径规划方法,包括初始化模型、超参数、环境,选择探索策略并以当前样本更新模型,更新值函数、策略和当前状态,判断当前情节是否结束进而利用当前采样轨迹更新轨迹池,利用重构采样轨迹更新轨迹池,然后由轨迹池中所有轨迹来更新模型,采用模型进行规划,判断是否达到最大情节数,最后根据学习到最优策略来来获取清洁机器人规划的最优路径。本发明通过采用采样轨迹和单个样本同时对模型进行更新,提高模型学习的精度,同时利用该模型进行规划,提高值函数、策略和整个算法的学习速度,同时提高样本的利用效率,实现在更短的时间内采用更少的样本来获得清洁机器人进行规划的最优路径。
 法律状态
法律状态
| 法律状态公告日 | 20191108 |
| 法律状态 | 授权 |
| 法律状态信息 | 授权 |
| 法律状态公告日 | 20181130 |
| 法律状态 | 实质审查的生效 |
| 法律状态信息 | 实质审查的生效 IPC(主分类):G05D 1/02 申请日:20180426 |
| 法律状态公告日 | 20181106 |
| 法律状态 | 公开 |
| 法律状态信息 | 公开 |
| 法律状态公告日 | 20181106 |
| 法律状态 | 公开 |
| 法律状态信息 | 公开 |
 权利要求
权利要求
权利要求数量(7)
独立权利要求数量(1)
1.一种基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,包括一下步骤:
步骤1)、初始化模型,设置环境的状态空间X和动作空间U;
步骤2)、初始化超参数,设置折扣率γ,衰减因子λ,情节数,高斯函数的探索方差,每个情节所包含的最大时间步,值函数的学习率,策略的学习率,模型的学习率,规划的次数;
步骤3)、初始化环境,设置机器人的当前状态x和边界位置,以及环境中所有的障碍物和垃圾位置;
步骤4)、选择探索策略:选择高斯函数N(u,σ)作为动作选择策略,即以当前最优动作u作为高斯函数的均值,以探索项作为高斯函数的方差,选择当前状态下清洁机器人执行的动作u;
步骤5)、获取当前样本:在当前状态x下,执行步骤(4)中确定的动作u,得到清洁机器人的下一个状态x',立即奖赏r;
步骤6)、采用当前样本更新模型:更新近似模型中的状态迁移函数和奖赏函数参数向量;
步骤7)、更新值函数:更新值函数的参数向量;
步骤8)、更新策略:更新策略的参数向量;
步骤9)、更新采样轨迹:将当前样本(x,u,x',r)加入当前采样路径中(x,u,x',r),(x,u,x',r),...,(x,u,x',r);
步骤10)、更新当前状态:x=x';
步骤11)、判断当前情节是否结束:如果结束,转入步骤12),否则转入步骤4);
步骤12)、利用当前采样轨迹更新轨迹池:将当前采样轨迹(x,u,x',r),(x,u,x',r),...,(x,u,x',r)加入到轨迹池D中:
步骤13)、利用重构采样轨迹更新轨迹池:利用当前采样轨迹构建模拟轨迹(x,u,x',r),(x,u,x',r),...,(x,u,x',r),并重构该轨迹,将重构的轨迹(x',u,x,r),(x',u,x,r),...,(x',u,x,r)加入到轨迹池D中;
步骤14)、采用轨迹池中所有轨迹来更新模型;
步骤15)、采用模型进行规划;
步骤16)、判断是否达到最大情节数:如果达到,转入步骤17),否则转入步骤3)继续执行;
步骤17)、根据学习到的最优策略来来获取清洁机器人规划的最优路径。
2.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(6)中的状态迁移函数和奖赏函数的近似公式为x=φ(x,u)θ和r=φ(x,u)υ,其中,θ为状态迁移函数的参数向量,υ为奖赏函数的参数向量,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
3.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(7)中的值函数的近似公式为:采用梯度下降法进行更新,其参数向量为:
4.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(8)中的策略的近似公式为:采用梯度下降法进行更新,其参数向量为
5.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(13)中的模拟轨迹即获取真实轨迹的初始状态和实际发生的动作序列,并利用学习的模型x=φ(x,u)θ和r=φ(x,u)υ来对下一个状态和奖赏进行预测,递归进行预测后将生成整个模拟的采样序列,其中φ为采用高斯函数表示的状态动作对的特征。
6.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(14)中基于轨迹池的模型更新方式为:对于轨迹池中的所有轨迹,以及轨迹中的每个样本,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
7.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(15)是在一定的规划次数下,迭代地利用模型x=φ(x,u)θ和r=φ(x,u)υ生成下一个状态和奖赏,并利用下一个状态和奖赏来更新值函数参数向量和策略参数向量和ζ=ζ+α(r+γV(x)-V(x))(u-u*)(x),其中,为高斯函数表示的状态特征。
1.一种基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,包括一下步骤:
步骤1)、初始化模型,设置环境的状态空间X和动作空间U;
步骤2)、初始化超参数,设置折扣率γ,衰减因子λ,情节数,高斯函数的探索方差,每个情节所包含的最大时间步,值函数的学习率,策略的学习率,模型的学习率,规划的次数;
步骤3)、初始化环境,设置机器人的当前状态x和边界位置,以及环境中所有的障碍物和垃圾位置;
步骤4)、选择探索策略:选择高斯函数N(u*,σ)作为动作选择策略,即以当前最优动作u*作为高斯函数的均值,以探索项作为高斯函数的方差,选择当前状态下清洁机器人执行的动作u;
步骤5)、获取当前样本:在当前状态x下,执行步骤(4)中确定的动作u,得到清洁机器人的下一个状态x',立即奖赏r;
步骤6)、采用当前样本更新模型:更新近似模型中的状态迁移函数和奖赏函数参数向量;
步骤7)、更新值函数:更新值函数的参数向量;
步骤8)、更新策略:更新策略的参数向量;
步骤9)、更新采样轨迹:将当前样本(x,u,x',r)加入当前采样路径中(x0,u0,x0',r0),(x1,u1,x1',r1),...,(x,u,x',r);
步骤10)、更新当前状态:x=x';
步骤11)、判断当前情节是否结束:如果结束,转入步骤12),否则转入步骤4);
步骤12)、利用当前采样轨迹更新轨迹池:将当前采样轨迹(x0,u0,x0',r0),(x1,u1,x1',r1),...,(xn,un,xn',rn)加入到轨迹池D中:
步骤13)、利用重构采样轨迹更新轨迹池:利用当前采样轨迹构建模拟轨迹(x0,u0,x0,p',r0,p),(xop,u1,x1,p',r1,p),...,(xn-1,p,un,xn,p',rn,p),并重构该轨迹,将重构的轨迹(x0,p',u1,x1,r1),(x1,p',u1,x2,r2),...,(x'n-1,p,un,xn,rn)加入到轨迹池D中;
步骤14)、采用轨迹池中所有轨迹来更新模型;
步骤15)、采用模型进行规划;
步骤16)、判断是否达到最大情节数:如果达到,转入步骤17),否则转入步骤3)继续执行;
步骤17)、根据学习到的最优策略来来获取清洁机器人规划的最优路径。
2.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(6)中的状态迁移函数和奖赏函数的近似公式为xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt,其中,θ为状态迁移函数的参数向量,υ为奖赏函数的参数向量,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
3.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(7)中的值函数的近似公式为:采用梯度下降法进行更新,其参数向量为:
4.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(8)中的策略的近似公式为:采用梯度下降法进行更新,其参数向量为
5.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(13)中的模拟轨迹即获取真实轨迹的初始状态和实际发生的动作序列,并利用学习的模型xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt来对下一个状态和奖赏进行预测,递归进行预测后将生成整个模拟的采样序列,其中φ为采用高斯函数表示的状态动作对的特征。
6.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(14)中基于轨迹池的模型更新方式为:对于轨迹池中的所有轨迹,以及轨迹中的每个样本,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
7.根据权利要求1所述的基于近似模型多步优化的清洁机器人最优路径规划方法,其特征在于,步骤(15)是在一定的规划次数下,迭代地利用模型xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt生成下一个状态和奖赏,并利用下一个状态和奖赏来更新值函数参数向量和策略参数向量和ζt+1=ζt+α2(r+γV(xt+1)-V(xt))(u-u*)T(xt),其中,为高斯函数表示的状态特征。
 说明书
说明书
技术领域
本发明涉及一种清洁机器人路径规划方法,特别是涉及一种基于近似模型多步优化的清洁机器人最优路径规划方法。
背景技术
清洁机器人的自主路径规划问题,是控制领域中的一个常见问题。该问题可以将机器人所有可能的状态建模为状态空间,将其可以发生的所有动作建模为动作空间,将当前状态发生动作后达到的下一个可能状态建模为迁移函数,并将到达下一个状态所获得的立即奖赏建模为奖赏函数,即将该问题转换为一个马尔科夫决策过程。解决该问题的常规思路是采用离散的强化学习方法,如Q学习和SARSA算法来求解,如直接离散状态空间和动作空间,即将状态空间划分为若干的格子,将动作空间转换为向上、向下、向左和向右的动作,即将清洁机器人的规划问题转换为迷宫的最短路径规划问题。该方法对于小规模的状态空间是切实可行的,但是当状态空间足够大,同时障碍物分布复杂时,采用该方法无法获取清洁机器人的最优路径。
策略搜索是一种应用于连续状态和动作空间的强化学习方法,行动者评论家方法在策略搜索算法的基础上,加入了值函数的估计,可以更快地获取连续空间的最优行为策略,是解决连续空间问题的一种有效方法。然而,无论是策略搜索算法还是行动者评论家算法都属于模型无关的算法,即直接通过机器人与环境交互获取的样本来学习值函数策略,需通过大量样本才能学习到一个较好的策略,因此,具有样本效率不高的缺点。
模型相关的学习方法假设模型事先存在,该类方法具有较高的样本效率,通常能利用模型进行规划来加速策略的求解。然而,现实世界中的大部分问题中,模型事先是未知的,如果利用模型规划来加速策略或整个算法的收敛过程,那么就需要实现学习一个模型。当学习的模型足够精确时,能加速策略和算法的收敛,而当学习的模型不够精确时,利用该模型来进行规划,反而会阻碍策略的最优解的获取。
发明内容
针对上述现有技术缺陷,本发明的任务在于提供一种基于近似模型多步优化的清洁机器人最优路径规划方法,在较短时间内学习一个更精确的模型,并利用模型和在线学习来获得清洁机器人进行规划的最优路径。
本发明技术方案是这样的:一种基于近似模型多步优化的清洁机器人最优路径规划方法,包括以下步骤:
步骤1)、初始化模型,设置环境的状态空间X和动作空间U;
步骤2)、初始化超参数,设置折扣率γ,衰减因子λ,情节数,高斯函数的探索方差,每个情节所包含的最大时间步,值函数的学习率,策略的学习率,模型的学习率,规划的次数;
步骤3)、初始化环境,设置机器人的当前状态x和边界位置,以及环境中所有的障碍物和垃圾位置;
步骤4)、选择探索策略:选择高斯函数N(u*,σ)作为动作选择策略,即以当前最优动作u*作为高斯函数的均值,以探索项作为高斯函数的方差,选择当前状态下清洁机器人执行的动作u;
步骤5)、获取当前样本:在当前状态x下,执行步骤(4)中确定的动作u,得到清洁机器人的下一个状态x',立即奖赏r;
步骤6)、采用当前样本更新模型:更新近似模型中的状态迁移函数和奖赏函数参数向量;
步骤7)、更新值函数:更新值函数的参数向量;
步骤8)、更新策略:更新策略的参数向量;
步骤9)、更新采样轨迹:将当前样本(x,u,x',r)加入当前采样路径中(x0,u0,x0',r0),(x1,u1,x1',r1),...,(x,u,x',r);
步骤10)、更新当前状态:x=x';
步骤11)、判断当前情节是否结束:如果结束,转入步骤12),否则转入步骤4);
步骤12)、利用当前采样轨迹更新轨迹池:将当前采样轨迹(x0,u0,x0',r0),(x1,u1,x1',r1),...,(xn,un,xn',rn)加入到轨迹池D中:
步骤13)、利用重构采样轨迹更新轨迹池:利用当前采样轨迹构建模拟轨迹(x0,u0,x0,p',r0,p),(xop,u1,x1,p',r1,p),...,(xn-1,p,un,xn,p',rn,p),并重构该轨迹,将重构的轨迹(x0,p',u1,x1,r1),(x1,p',u1,x2,r2),...,(x'n-1,p,un,xn,rn)加入到轨迹池D中;
步骤14)、采用轨迹池中所有轨迹来更新模型;
步骤15)、采用模型进行规划;
步骤16)、判断是否达到最大情节数:如果达到,转入步骤17),否则转入步骤3)继续执行;
步骤17)、根据学习到的最优策略来获取清洁机器人规划的最优路径。
作为优选的技术方案,步骤(6)中的状态迁移函数和奖赏函数的近似公式为xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt,其中,θ为状态迁移函数的参数向量,υ为奖赏函数的参数向量,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
作为优选的技术方案,步骤(7)中的值函数的近似公式为:采用梯度下降法进行更新,其参数向量为:
作为优选的技术方案,步骤(8)中的策略的近似公式为:采用梯度下降法进行更新,其参数向量为:
作为优选的技术方案,步骤(13)中的模拟轨迹即获取真实轨迹的初始状态和实际发生的动作序列,并利用学习的模型xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt来对下一个状态和奖赏进行预测,递归进行预测后将生成整个模拟的采样序列,其中φ为采用高斯函数表示的状态动作对的特征。
作为优选的技术方案,步骤(14)中基于轨迹池的模型更新方式为:对于轨迹池中的所有轨迹,以及轨迹中的每个样本,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
作为优选的技术方案,步骤(15)是在一定的规划次数下,迭代地利用模型xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt生成下一个状态和奖赏,并利用下一个状态和奖赏来更新值函数参数向量和策略参数向量和ζt+1=ζt+α2(r+γV(xt+1)-V(xt))(u-u*)T(xt),其中,为高斯函数表示的状态特征。
本发明与现有技术相比的优点在于:
(1)采用高斯函数表示状态动作特征,并通过线性函数逼近器来组合该特征以及参数向量,使得该模型表示方法,不仅具有线性函数逼近器的形式简单的优点,同时所需样本量更少。由于组合了高斯函数表示的特征,使得该线性函数逼近器的表示能力大为增加。
(2)采用采样轨迹和样本同时对模型进行更新。当机器人获取一条完整的路径后,再利用该条轨迹和样本同时对模型更新,同时利用单步更新和多步更新,以提高模型进行单步和多步预测的能力。
针对较为大规模和复杂的清洁机器人行为规划问题,本发明方法在行动者-评论家的框架内,通过对模型的表示方法以及模型更新阶段的多步更新机制进行设计,使得学习的模型具有较高的精确度。当利用较为精确的近似模型来进行规划时,可以明显地促进策略和算法收敛,从而实现清洁机器人更好地避障和寻找最优路径。
附图说明
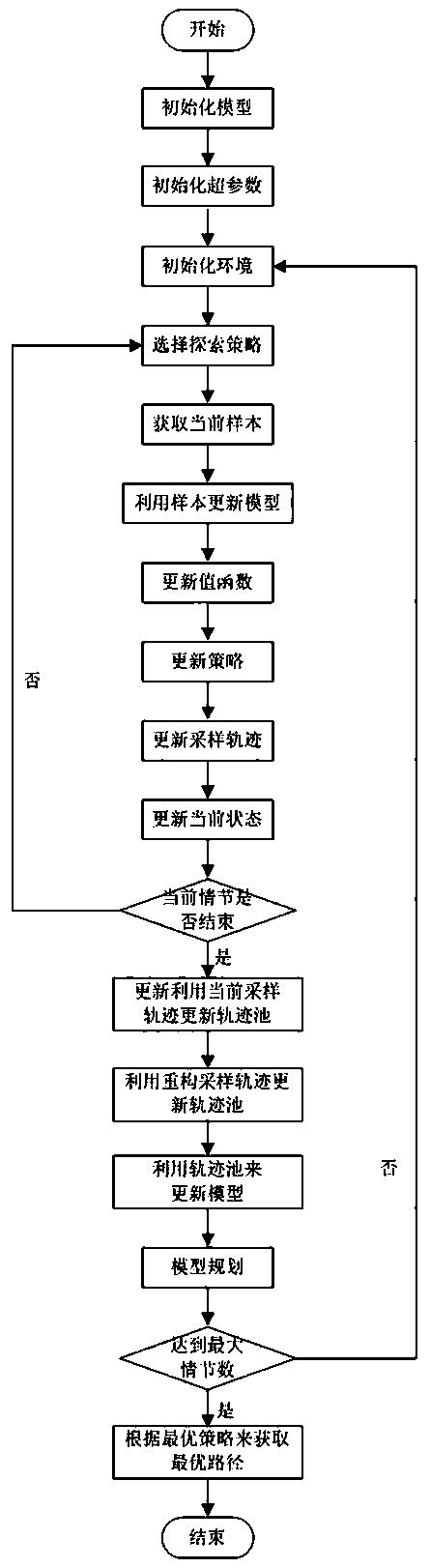
图1为本发明方法流程示意图;
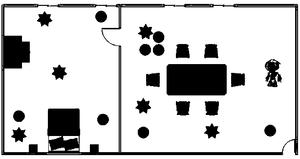
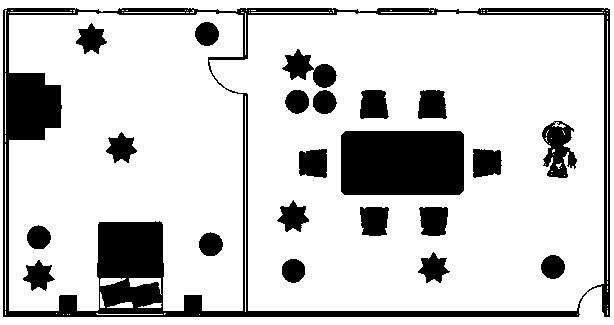
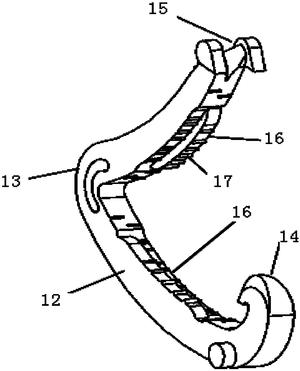
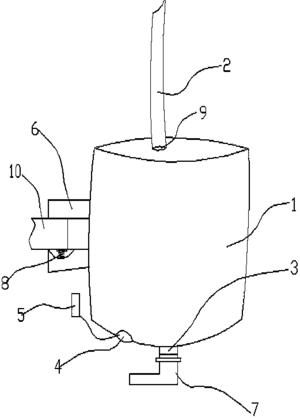
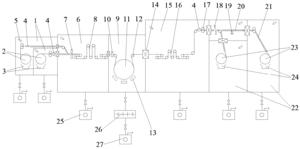
图2为本发明实施例中的布局示意图;
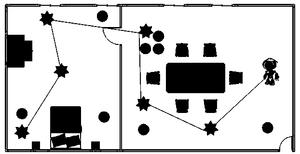
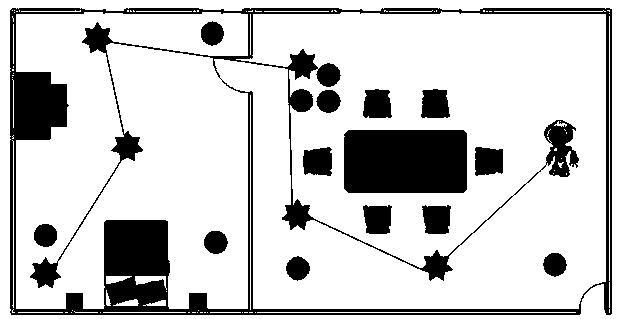
图3为本发明实施例中生成的某条最优路径示意图。
具体实施方式
下面结合实施例对本发明作进一步说明,但不作为对本发明的限定。
请结合图1所示,本实施例涉及的基于近似模型多步优化的清洁机器人最优路径规划方法,包括以下步骤:
步骤1)、初始化模型,设置环境状态空间X为两个房间的水平和垂直坐标的界限值,动作空间U中的动作为机器人沿着[-π,+π]角度进行移动一个定值;
步骤2)、初始化超参数,设置折扣率γ=0.9,衰减因子λ=0.9,情节数=200,高斯函数的探索方差为0.2,每个情节所包含的最大时间步为200,值函数的学习率为0.6,策略的学习率为0.6,模型的学习率为0.5,规划的次数为100;
步骤3)、初始化环境,设置机器人的当前状态x和边界位置,以及环境中所有的障碍物和垃圾位置;
步骤4)、选择探索策略:选择高斯函数N(u*,0.2)作为动作选择策略,获得当前状态下清洁机器人执行的动作u;
步骤5)、在当前状态x下,执行步骤(4)中确定的动作u,得到清洁机器人的下一个状态x',立即奖赏r,从而生成当前样本(x,u,x',r);
步骤6)、状态迁移函数和奖赏函数的近似公式为xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt,其中,θ为状态迁移函数的参数向量,υ为奖赏函数的参数向量,采用单步的预测误差作为梯度信号,由当前样本(x,u,x',r)得到参数向量的更新公式为:和
步骤7)、更新值函数:值函数的近似公式为:由当前样本(x,u,x',r)采用梯度下降法进行更新,其参数向量为:
步骤8)、更新策略:策略的近似公式为:由当前样本(x,u,x',r)采用梯度下降法进行更新,其参数向量为:
步骤9)、更新采样轨迹:将当前样本(x,u,x',r)加入当前采样路径中(x0,u0,x0',r0),(x1,u1,x1',r1),...,(x,u,x',r);
步骤10)、更新当前状态:x=x';
步骤11)、更新当前时间步(递增1),如果已经达到最大时间步200或者已实现目标,则情节结束,转入步骤12);否则转入步骤4);
步骤12)、利用当前采样轨迹更新轨迹池:将当前采样轨迹(x0,u0,x0',r0),(x1,u1,x1',r1),...,(xn,un,xn',rn)加入到轨迹池D中:
步骤13)、利用重构采样轨迹更新轨迹池:利用当前采样轨迹构建模拟轨迹(x0,u0,x0,p',r0,p),(xop,u1,x1,p',r1,p),...,(xn-1,p,un,xn,p',rn,p),并重构该轨迹,将重构的轨迹(x0,p',u1,x1,r1),(x1,p',u1,x2,r2),...,(x'n-1,p,un,xn,rn)加入到轨迹池D中;模拟轨迹即获取真实轨迹的初始状态和实际发生的动作序列,并利用学习的模型xt+1=φT(xt,ut)θt和rt+1=φT(xt,ut)υt来对下一个状态和奖赏进行预测,递归进行预测后将生成整个模拟的采样序列,其中φ为采用高斯函数表示的状态动作对的特征;
步骤14)、对于轨迹池中的所有轨迹,以及轨迹中的每个样本,采用单步的预测误差作为梯度信号,得到参数向量的更新公式为:和
步骤15)、采用模型进行100次规划,即迭代地利用模型和rt+1=φT(xt,ut)υt生成下一个状态和奖赏,并利用下一个状态和奖赏来更新值函数参数向量和策略参数向量和ζt+1=ζt+α2(r+γV(xt+1)-V(xt))(u-u*)T(xt),其中,为高斯函数表示的状态特征;
步骤16)、判断情节是否达到最大值200:如果达到,转入步骤17),否则转入步骤3)继续执行;
步骤17)、根据学习到最优策略来获取清洁机器人规划的最优路径。
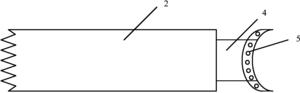
参见图2所示,清洁机器人的活动范围是左边的卧室和右边的客厅,清洁机器人当前在右边的客厅中,客厅中有餐桌和沙发等家具,除此之外还有一些随机摆放的障碍物(圆形所示),地面上有一些需要清扫的垃圾(星形图所示)。清洁机器人的目标就是在避开家具和障碍物的条件下,将客厅和卧室的垃圾清扫完毕。根据房间的布置,清洁机器人在打扫完客厅后,需要经过中间的房门才能顺利进入卧室。机器人头部均匀地安装有距离传感器,每个传感器都能探测其正前方1单位长度内是否有障碍物。清洁机器人在房间中初始位置是随机的,它的目标是尽可能快地打扫完所有的垃圾,当该目标被实现后,清洁机器人会获得的奖赏值为10;当在房间中碰到障碍物时,会得到一个-20的奖赏;其它情况下获得的立即奖赏为-1。当扫地机器人在图1所示的初始位置时,采用本专利在该场景中实施后,得到的一条最优的清扫路径如图3所示。
 价值度评估
价值度评估
技术价值
经济价值
法律价值
0 0 055.0分
0 50 75 100专利价值度是通过科学的评估模
型对专利价值进行量化的结果,
基于专利大数据针对专利总体特
征指标利用计算机自动化技术对
待评估专利进行高效、智能化的
分析,从技术、经济和法律价值
三个层面构建专利价值评估体
系,可以有效提升专利价值评估
的质量和效率。
总评:55.0分
该专利价值中等 (仅供参考)
本专利文献中包含【1 个实施例】、【1 个技术分类】,从一定程度上而言上述指标的数值越大可以反映出所述专利的技术保护及应用范围越广。 【专利权的维持时间6 年】专利权的维持时间越长,其价值对于权利人而言越高。
技术价值 29.0
该指标主要从专利申请的著录信息、法律事件等内容中挖掘其技术价值,专利类型、独立权利要求数量、无效请求次数等内容均可反映出专利的技术性价值。 技术创新是专利申请的核心,若您需要进行技术借鉴或寻找可合作的项目,推荐您重点关注该指标。
部分指标包括:
授权周期(发明)
18 个月独立权利要求数量
1 个从属权利要求数量
6 个说明书页数
5 页实施例个数
1 个发明人数量
5 个被引用次数
0 次引用文献数量
0 个优先权个数
0 个技术分类数量
1 个无效请求次数
0 个分案子案个数
0 个同族专利数
0 个专利获奖情况
无保密专利的解密
否经济价值 7.0
该指标主要指示了专利技术在商品化、产业化及市场化过程中可能带来的预期利益。 专利技术只有转化成生产力才能体现其经济价值,专利技术的许可、转让、质押次数等指标均是其经济价值的表征。 因此,若您希望找到行业内的运用广泛的热点专利技术及侵权诉讼中的涉案专利,推荐您重点关注该指标。
部分指标包括:
申请人数量
1申请人类型
院校许可备案
0 次权利质押
0 次权利转移
0 个海关备案
否法律价值 19.0
该指标主要从专利权的稳定性角度评议其价值。专利权是一种垄断权,但其在法律保护的期间和范围内才有效。 专利权的存续时间、当前的法律状态可反映出其法律价值。故而,若您准备找寻权属稳定且专利权人非常重视的专利技术,推荐您关注该指标。
部分指标包括:
存活期/维持时间
6法律状态
有权-审定授权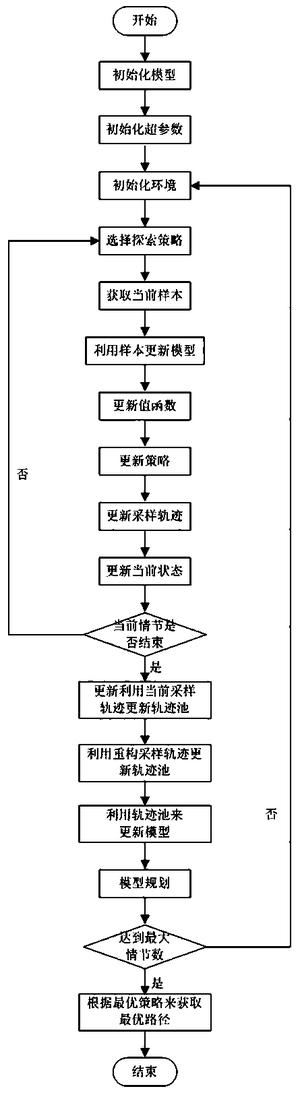
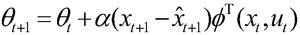
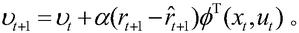
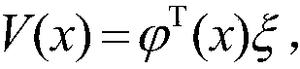
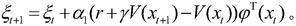
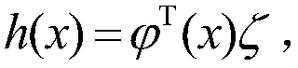
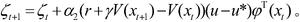
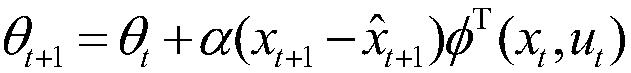
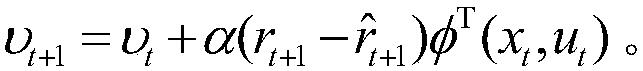
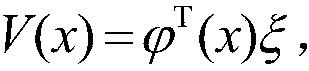
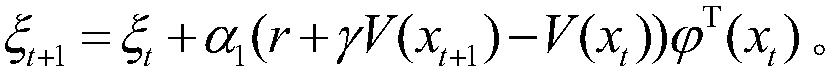
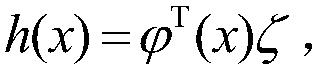
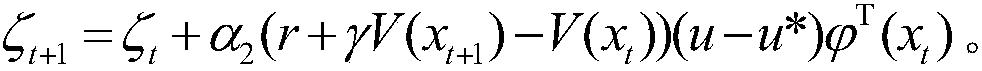








 苏公网安备 32041202001399号
苏公网安备 32041202001399号



 loading...
loading...